1、实验题  13．在研究平抛运动的实验中，用一张印有小方格的纸记录轨迹。小方格的边长L=1.25cm，若小球在平抛运动中先后经过的几个位置如右图所示的a、b、c、d四个点，则小球的初速度计算表达式为v0= ?（用L和g表示），其值为?m/s.（g=9.8m/s2，0.352=0.1225）。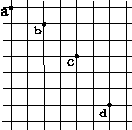

参考答案：略

本题解析：略

本题难度：简单

2、计算题  某人驾驶摩托车匀速行驶至某处遇到5m宽的沟，若对面比此处低4.9m，则此人驾车的速度至少要多大才能安全跃过此沟？（g="9.8" m/s2）

参考答案：5 m/s

本题解析：

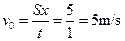
∴?驾车速度至少为5 m/s

本题难度：简单

3、简答题  如图所示，水平屋顶高H=5m，墙高h=3.75m，墙到房子的距离L=3.6m，墙外马路宽x=7.4m，小球从房顶水平飞出落在墙外的马路上，求小球离开房顶时的速度．（取g=10m/s2）

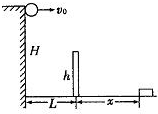
参考答案：若v太大，小球落在马路外边，因此，球落在马路上，v的最大值vmax为球落在马路最右侧A点时的平抛初速度，小球做平抛运动，设运动时间为t1．
则小球的水平位移：L+x=vmaxt1，
小球的竖直位移：H=12gt12
解以上两式得：vmax=（L+x）

本题解析：

本题难度：一般

4、计算题  如图所示，有一长为L的细线，细线的一端固定在O点，另一端拴一质量为m的小球，现使小球恰好在竖直平面内做完整的圆周运动，已知水平面上的C点在O点的正下方，且到O点的距离为1.9 L，不计空气阻力，求：(g＝10 m/s2)

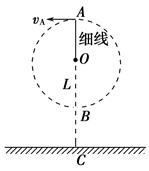
(1)小球通过最高点A的速度vA；
(2)若小球通过最低点B时，细线对小球的拉力T恰好为小球重力的6倍，且小球通过B点时细线断裂，求小球落地点到C的距离．

参考答案：(1)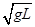　(2)3L

本题解析：(1)对小球，当恰好通过最高点时，细线的拉力为0，根据向心力公式有mg＝m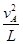，则vA＝.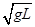
(2)当小球在B点时，由牛顿第二定律得
T－mg＝m，而T＝6mg
解得小球在B点的速度vB＝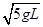
细线断裂后，小球做平抛运动，则
竖直方向：1.9L－L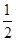＝gt2
水平方向：x＝vBt
代入数据得：x＝3L，即小球落地点到C的距离为3L.

本题难度：简单

5、简答题  将小球从离地面5m高处、向离小球4m远的竖直墙以8m/s的初速度水平抛出，不计空气阻力．求：（g=10m/s2）
（1）小球碰墙点离地面的高度；
（2）要使小球不碰墙，小球的最大初速度．

参考答案：（1）小球作平抛运动，水平方向做匀速直线运动，则有：
x=v0t
得小球碰墙的时间为：t=xv0=48s=0.5s
竖直方向做自由落体运动，所以有：
h=12gt2=12×10×0.25m=1.25m
可得小球碰墙点离地面的高度为：
h0=H-h=5-1.25m=3.75m?
（2）设小球恰好击中墙角时小球的初速度为v0′，由平抛运动规律
水平方向：s=v0′t′
竖直方向：H=12gt′2?
得：v0′=s

本题解析：

本题难度：一般