1、选择题  如图在光滑地面上，水平外力F拉动小车和木块一起做无相对滑动的匀加速运动。小车质量是M，木块质量是m，力大小是F，加速度大小是a，木块和小车之间动摩擦因数是μ，则在这个过程中，木块受到的摩擦力大小是：（?）

A．ma
B．μma
C．
D．F-Ma

参考答案：ACD

本题解析：A、根据牛顿第二定律可知，木块受到的摩擦力即为木块受到的合外力ma；正确
B、由于小车和木块一起做无相对滑动的匀加速运动，所以木块受到的是静摩擦力，与μ无关；错误
C、把小车和木块看成一个整体，加速度，木块受到的摩擦力即为木块受到的合外力，所以；正确
D、以小车为研究对象，设小车受到的摩擦力为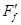，则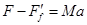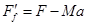，，根据牛顿第三定律，木块受到的摩擦力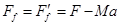；正确
故选ACD
点评：当分析多个物体的受力、运动情况时，通常可以采用整体法和隔离法，用整体法可以求得系统的加速度的大小，再用隔离法可以求物体之间的作用的大小．

本题难度：一般

2、计算题  消防队员为缩短下楼的时间，往往抱着竖直的杆直接滑下．假设一名质量为60 kg、训练有素的消防队员从七楼(即离地面18 m的高度)抱着竖直的杆以最短的时间滑下．已知杆的质量为200 kg，消防队员着地的速度不能大于6 m/s，手和腿对杆的最大压力为1 800 N，手和腿与杆之间的动摩擦因数为0.5，设当地的重力加速度g＝10 m/s2.假设杆是固定在地面上的，杆在水平方向不移动．试求：
(1)消防队员下滑过程中的最大速度；
(2)消防队员下滑过程中杆对地面的最大压力；
(3)消防队员下滑的最短的时间．

参考答案：(1) vm＝12 m/s(2) 2.4 s

本题解析：(1)消防队员开始阶段自由下落的末速度即为下滑过程的最大速度vm，有2gh1＝v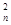
消防队员受到的滑动摩擦力
Ff＝μFN＝0.5×1 800 N＝900 N.
减速阶段的加速度大小：
a2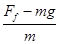＝＝5 m/s2
减速过程的位移为h2，由v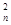－v2＝2a2h2
又h＝h1＋h2
以上各式联立可得：vm＝12 m/s.
(2)以杆为研究对象得：
FN＝Mg＋Ff＝2 900 N.
根据牛顿第三定律得，杆对地面的最大压力为2 900 N.
(3)最短时间为
tmin＝＋＝2.4 s.
本题考查的是牛顿运动定律，解决本题的关键是弄清楚人的运动过程，人先沿着杆做自由落体运动，即人和杆之间没有作用力，然后沿杆减速下降，即在杆给的摩擦力与重力的作用下做减速运动，而且还要保证人落地速度不能大于6 m/s，要求下落过程中的最大速度，即消防队员开始阶段自由下落的末速度即为下滑过程的最大速度，列出自由落体过程的等式，和减速下降过程的等式，联立即可求出。杆给人一向上的摩擦力，根据牛顿第三定律，人给杆一个下的摩擦力，地对杆的支持力的大小为杆的重力与杆受到的摩擦力之和，整个下落过程时间最短，那么就是落地时速度正好是6m/s的情况，即时间为自由落体时间与减速时间之和

本题难度：简单

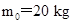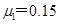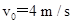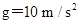3、选择题  质量为、长为L＝5 m的木板放在水平面上，木板与水平面的动摩擦因数为.将质量m＝10 kg的小木块(可视为质点)，以的速度从木板的左端水平抛射到木板上(如图所示)，小木块与木板面的动摩擦因数为?(最大静摩擦力等于滑动摩擦力，)．则以下判断中正确的是(　　)

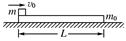
A．木板一定静止不动，小木块不能滑出木板
B．木板一定静止不动，小木块能滑出木板
C．木板一定向右滑动，小木块不能滑出木板
D．木板一定向右滑动，小木块能滑出木板

参考答案：A

本题解析：与地面间的摩擦力为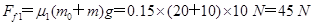，m与之间的摩擦力为，所以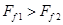，所以木板一定静止不动；小木板在木板上滑行的距离为x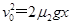，，解得，小木块不能滑出木板．
故选A
点评：解决本题的关键能正确地进行受力分析，结合牛顿第二定律和运动学公式进行求解．

本题难度：一般

4、选择题  某节能运输系统装置的简化示意图如图所示．小车在轨道顶端时，自动将货物装入车中，然后小车载着货物沿不光滑的轨道无初速下滑，并压缩弹簧．当弹簧被压缩至最短时，立即锁定并自动将货物卸下．卸完货物后随即解锁，小车恰好被弹回到轨道顶端，此后重复上述过程．则下列说法中正确的是（　　）
A．小车上滑的加速度大于下滑的加速度
B．小车每次运载货物的质量必须是确定的
C．小车上滑过程中克服摩擦阻力做的功等于小车下滑过程中克服摩擦阻力做的功
D．小车与货物从顶端滑到最低点的过程中，减少的重力势能部分转化为弹簧的弹性势能