1、选择题  如图所示，用光滑的粗铁丝做成一直角三角形，BC边水平，AC边竖直，∠ABC=β，AB及AC两边上分别套用有细线连着的铜环P、Q，当它们静止时，细线跟AB所成的角θ的大小为（细线长度小于BC）
A.θ=β
B.
C.θ＜β
D.β＜θ＜

参考答案：D

本题解析：分析：本题可以运用假设法分析θ与β的关系．假设AC上的环质量为零，则知平衡时θ=β；假设AB上的铜环P的质量为零，平衡时则有θ=，再分析两环有质量时的角度的关系．
解答：假设AC上的铜环质量为零，重力为零，它仅受线的拉力和铁丝AC的弹力，它们是一对平衡力．由于铁丝对AC上的环的弹力垂直于AC，则细线必定垂直于AC，则细线平行于BC，此时θ=α．但实际上AC上的环的质量大于零，重力大于零，要使此环处于静止，细线的左端必须斜向左上方，则有θ＞β．
假设AB上的铜环P的质量为零，重力为零，它仅受细线的拉力和铁丝AB的弹力，它们是一对平衡力，则此环平衡时，细线与AB垂直，θ=，而AB上的铜环的质量大于零，重力大于零，要使此环处于静止状态，细线不能与AB垂直，应有θ＜，故β＜θ＜．
故选D．
点评：本题运用假设法的思维方法，也可以通过分析两环的受力情况，由平衡条件，根据正交分解法确定θ的范围．

本题难度：简单

2、选择题  如图中a、b、c三个物块，M、N为两个轻质弹簧，R为跨过光滑定滑轮的轻绳，它们按图中方式连接并处于平衡状态,则下列说法中错误的是

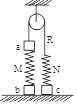
A.有可能N处于拉伸状态而M处于压缩状态；
B.有可能N处于压缩状态而M处于拉伸状态；
C.有可能N处于不伸不缩状态而M处于压缩状态；
D.有可能N处于拉伸状态而M处于不伸不缩状态。

参考答案：B

本题解析：试题分析：由于N弹簧上面与细线相连，故N弹簧可能处于原长也可能被拉伸；
当N弹簧处于原长时，细线的拉力为零，M弹簧在a物体的作用下处于压缩状态，故A正确；
当N弹簧处于拉伸状态时，细线对a又拉力，当拉力小于a物体的重力时，M弹簧处于压缩状态；当拉力等于a物体的重力时，M弹簧处于原长状态；当拉力大于a物体的重力时，M弹簧处于伸长状态；故D正确；
从上面的分析中发现共有四种情况，即：
①N处于伸长状态而M处于压缩状态；②N处于伸长状态而M处于伸长状态；
③N处于伸长状态而M处于不伸长不压缩状态；④N与M都N处于不伸不缩状态；
故B、C选项中的状态不存在；
故选AD．
考点：考查了力的合成与分解的应用
点评：先分析N弹簧，由于上面与细线相连，故N弹簧可能处于原长也可能被拉伸，然后分这两种情况去分析M弹簧

本题难度：困难

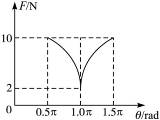
3、选择题  图1-5-16是两个共点力的合力F跟两个分力的夹角θ的关系图象，下面的分析中正确的是
?
图1-5-16 ? ? ? ? ? ? ? ? ? ? ? ? ?
A.F的取值范围是2 N≤F≤10 N
B.F的取值范围是4 N≤F≤14 N
C.两个分力分别是6 N和8 N
D.两个分力分别是2 N和10 N

参考答案：C

本题解析：设两个分力分别为F1和F2，从图示可以看出，两个力的夹角为180°时，合力F为2 N，得到F1-F2=2 N；当两个力间的夹角为90°时，合力F为10 N，得到F1+F2=14 N，由以上两式得，F1=6 N，F2=8 N或F1=8 N，F2=6 N，所以F的取值范围为2 N≤F≤14 N，故正确答案只有C

本题难度：简单

4、选择题 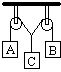 如图所示．A，B质量相等，均为m，C质量为M（M＞m），C对A，B是对称的．三个物体处于图中所示的平衡位置，下列说法正确的是
A.将C物体向下拉一小段距离，松手后，三物体仍能回到原来的位置，再?次达到平衡
B.若C物的质量增加，则三物体将可能有一个新的平衡位置
C.若C物的质量减小，则三物体将可能有一个新的平衡位置
D.以上三种情况，都无法再达到平衡

参考答案：ABC

本题解析：分析：三个物体处于图中所示的平衡位置时说明AB对绳子拉力的合力与C的重力相等，当C上升或下降后根据AB绳子夹角的变化结合平行四边形定则来判断合力的变化从而判断是否可以重新平衡
解答：三个物体处于图中所示的平衡位置时说明AB对绳子拉力的合力与C的重力相等
A、若C物体下拉一段距离，AB绳子上的拉力不变，但夹角变小，则两拉力的合力变大，松手后C将上升到原来的位置再次达到平衡，故A正确；
B、若C 的质量增加，C绳子的拉力增大，C将拉着结点向下移动，下移后AB绳子拉力的夹角变小，则合力变大，当合力增大到与C重力相等的时候，重新达到平衡，故C正确；
C、若C的质量减小，则C绳子的拉力减小，结点将向上移动，上移后AB绳子的夹角增大，则AB绳子拉力的合力减小，当合力减小到与C重力相等的时候，重新达到平衡，故C正确；则D错误．
故选：ABC．
点评：本题考查平行四边形定则进行力的合成，分力不变，夹角变大时合力变大．

本题难度：困难

5、选择题 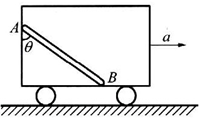 如图所示，在以一定加速度a行驶的车厢内，有一长为L、质量为m的棒AB靠在光滑的后壁上，棒与厢底面之间的动摩擦因数为μ，为了使棒不滑动，棒与竖直平面所成的夹角为θ，则tanθ的值可取
A.
B.
C.
D.

参考答案：ACD

本题解析：分析：棒与车具有相同的加速度，当棒与竖直平面所成的夹角最大时，有向左的最大静摩擦力，夹角最小时，有向右的最大静摩擦力，根据牛顿第二定律求出车厢后壁对棒的弹力，在根据力矩平衡求出临界的角度．
解答：设在A、B处的弹力大小各是FA、FB，在B处静摩擦力大小是 f．
当夹角θ取较大的数值θ大时，棒将发生A向下、B向右滑动，这时 f 的方向是水平向左．
由牛顿第二定律得：FA1-f=ma　且　f=μFB，FB=mg　（竖直方向不动）
得　FA1=m（a+μg）
车厢是非惯性系，在车厢里看棒受到非惯性力F惯=ma
以B点为轴，用合力矩为0得　FA1Lcosθ大=mg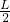sinθ大+ma
所以　tanθ大==
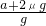
θ大=arc tan．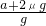
当夹角θ取较小的数值θ小时，棒将发生A向上、B向左滑动，这时 f 的方向是水平向右．
由牛顿第二定律得　FA2+f=ma　且　f=μFB，FB=mg　（竖直方向不动）
得　FA2=m（a-μg）
以B点为轴，用合力矩为0得　FA2Lcosθ小=mg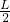sinθ小+ma
所以　tanθ小==
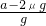
θ小=arc tan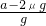
综上所述，夹角θ应在的范围是：
arc tan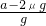≤θ≤arc tan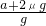．故A、C、D正确，B错误．
故选ACD．
点评：本题综合考查了牛顿第二定律和力矩平衡，综合性较强，以及考查了非惯性系问题，增加了题目的难度，要考虑棒会受到非惯性力．

本题难度：简单