1、简答题  如图所示，斜面顶端距水平面高度为h，质量为m1的小物块A从斜面顶端由静止滑下，进入水平滑道时无机械能损失，为使A制动，将轻弹簧的一端固定在水平滑道左端M处的墙上，另一端与质量为m2挡板B相连，弹簧处于原长时，B恰位于滑道上的O点．A与B碰撞时间极短，碰后结合在一起共同压缩弹簧，已知在OM段A、B与水平面间的动摩擦因数均为μ，其余各处的摩擦不计，重力加速度为g，求
（1）物块A在与挡板B碰撞前瞬间速度v的大小；
（2）物块A在与挡板B碰撞后瞬间速度v 的大小；
（3）弹簧最大压缩量为d时的弹性势能Ep（设弹簧处于原长时弹性势能为零）．

参考答案：（1）由机械能守恒定律，有m1gh=12m1v2
v=

本题解析：

本题难度：一般

2、简答题  如图所示，在绝缘光滑水平面上，可视为质点的A、B两个带正电的小球相距为r，带电量分别为4q和q．B的质量为m，在库仑力作用下，两球从静止开始运动：起初，A的加速度大小为a、B的加速度大小为4a；经过一段时间后，B的加速度大小为a，速度达到v．试计算这时：
（1）两球间距是多少？
（2）A球的速度是多少？
（3）两电荷的电势能发生了什么变化，变化了多少？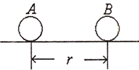

参考答案：（1）以B为研究对象，根据牛顿第二定律和库仑定律
K4q2r2=4ma，K4q2R2=ma，
所以，两球的间距为R=2r．
（2）根据两球受到同样大小的库仑力，有F=mAa=m×4a，可见，A的质量为mA=4m．
以两球组成的系统为研究对象，由动量守恒，又有mv+4mVA=0．
所以，A的速度为vA=-14V．
（3）根据电场力做正功，系统的电势能减少，据能量守恒得减少的电势能等于系统增加的动能，
所以△EP=EKA+EKB=12×4mV2A+12mV2=58mV2
答：（1）两球间距是2r．
（2）A球的速度是-14V
（3）两电荷的电势能减少58mV2

本题解析：

本题难度：一般

3、简答题  如图所示，A、B两物体叠放在一起以v0的速度沿光滑的水平轨道匀速运动，与静止在同一光滑水平轨道上的木板C发生碰撞，碰撞后B、C以相同的速度运动（不粘合），A滑上C后最终停在木板C的最右端，已知A、B、C质量均相等，A可看成质点，B、C的上表面相平，且B的上表面光滑，木板C长为L．
求：①A物体的最终速度；
②从A滑上木板C到A最终停在木板C最右端所经历的时间．

参考答案：①B、C碰撞过程动量守恒，以B的初速度方向为正方向，
由动量守恒定律得：mv0=（m+m）v，
A滑上C到A、C相对静止过程，A、C系统动量守恒，以A的初速度方向为正方向，
由动量守恒定律得：mv0+mv=（m+m）v′，
解得：v=v02，v′=34v0；
②A、C相互作用过程中，由能量守恒定律得：
fL=12mv02+12mv2-12（m+m）v′2，
以向右为正方向，对A，由动量定理得：
-ft=mv′-mv0，解得：t=4Lv0；
答：①A物体的最终速度为34v0；
②从A滑上木板C到A最终停在木板C最右端所经历的时间为4Lv0．

本题解析：

本题难度：一般

4、选择题  物体在水平恒力F作用下，从静止开始沿水平面由A点运动了S米，到达B点，则
A.水平面光滑时，力F对物体做功的平均功率较大
B.水平面不光滑时，力F对物体做功的平均功率较大
C.水平面不光滑时，力F在B点的瞬时功率较大
D.水平面光滑与不光滑两种情况下，力F在B点的瞬时功率都相等

参考答案：A

本题解析：试题分析：当水平面光滑时，物体在力F的作用下做匀加速直线运动，由动能定理可求B点的速度比有摩擦力时大，又平均速度等于初末速度的平均值，故无摩擦时平均速度大，由功率，可知，此时平均功率较大．故A正确，B错误；水平面光滑时，由动能定理可求B点的速度比有摩擦力时大，由功率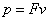，可知，此时平瞬时功率较大，故CD错误
故选A
考点：功率、平均功率和瞬时功率．
点评：当水平面光滑时，物体在力F的作用下做匀加速直线运动，平均速度等于初末速度的平均值，由动能定理可求B点的速度，由功率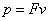，可求平均功率、瞬时功率；同理有摩擦时，摩擦力做负功B点的速度变小相应功率也变小．

本题难度：一般

5、选择题  水平冰面的同一直线上有三个木箱A、B、C，质量均为60kg.一质量为30kg的猴子停在A上，与A一起以3m/s的速度向右滑向静止的木箱B、C，在接近B时，以6m/s的水平速度跳上木箱B，接近木箱C时再以6m/s的水平对地速度跳上木箱C，最终与C一起运动，若木箱在运动过程中发生碰撞，则碰撞后不再分开，求木箱A、B、C最终运动的速度．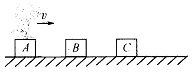

参考答案：vC=2m/s，方向向右。

本题解析：猴子跳离木箱A过程动量守恒，跳离后木箱速度为vA1，
（M+m）v0=mv+MvA1
解得：vA1=1.5m/s
猴子跳上木箱B后再跳离木箱B，B和猴子组成系统动量守恒
mv=mv+MvB1，解得vB1=0
A木箱将追上B木箱发生正碰，AB组成系统动量守恒，碰后速度为vAB，
MvA1=2MvAB，解得vAB=0.75m/s，方向水平向右，
猴子跳上木箱C过程，动量守恒：mv=（m+M）vC
解得vC=2m/s，方向向右。

本题难度：一般