1、计算题  一个右端开口左端封闭的U形玻璃管中装有水银，左侧封有一定质量的空气，如图所示，已知，空气柱长是40cm，两侧水银面高度差56cm，若左侧距管顶66cm处的k点处突然断开，断开处上方水银能否流出？这时左侧上方封闭气柱将变为多高？（设大气压强为1.013×105Pa）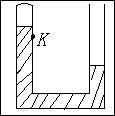

参考答案：否 ；16cm

本题解析：
?
断开处的压强小于外界大气压，故断开处上方的水银不会流出；以封闭的一定质量气体为研究对象：整个过程可以看做等温变化，由玻马定律：

可以求出：?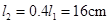
点评：此题要分析出K处断开后，压强和外界大气压相等,以密闭气体为研究对象，求出初、末态的压强，利用玻马定律。

本题难度：一般

2、简答题  一根长约为30cm、管内截面积为S=5.0×10-6m2的玻璃管下端有一个球形小容器，管内有一段长约1cm的水银柱．现在需要用比较准确的方法测定球形小容器的容积V．可用的器材有：刻度尺（量程500mm）、湿度计（测量范围0-100°C）、玻璃容器（高约为30cm，直径约10cm）、足够多的沸水和冷水．
（1）简要写出实验步骤及需要测量的物理量；
（2）说明如何根据所测得的物理量得出实验结果．

参考答案：（1）第一步：将水银柱以下的玻璃管浸没在沸水中，用温度计测出水温T1，用刻度尺测出玻璃管（除球形小容器）的长度l1；
? ?第二步：再将水银柱以下的玻璃管浸没在冷水中，用温度计测出水温T2，用刻度尺测出玻璃管（除球形小容器）的长度l2．
? （2）由于内部气体压强不变，根据盖吕萨克定律，得：
V1T1=V2T2?V+l1sT1=V+l2sT2，得V=T1l2-?T2l1T2-?T1s

本题解析：

本题难度：一般

3、选择题  如图所示，质量为M导热性能良好的气缸由一根平行于斜面的细线系在光滑斜面上。气缸内有一个质量为m的活塞，活塞与气缸壁之间无摩擦且不漏气。气缸内密封有一定质量的理想气体。如果大气压强增大（温度不变），则

A．气体的体积增大
B．细线的张力增大
C．气体的压强增大
D．斜面对气缸的支持力增大

参考答案：C

本题解析：对活塞受力分析，沿斜面方向可得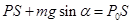：,所以 ,若P0增大，则P增大，根据PV=常量，可知V减小；对气缸和活塞的整体而言，细线的张力T=(M+m)gsinα,；斜面对气缸的支持力F=(M+m)gcosα。与大气压强无关。选项C正确。

本题难度：一般

4、简答题  长为L的均匀玻璃管受重力为G。管的内壁是光滑的。管内有一个横截面积为S的轻活塞.在管中封闭有一定质量的气体.用细线把活塞吊起来，管竖直静止时,管内气柱长为,大气压强为.如果想把玻璃管和活塞分离,缓慢向下拉动玻璃管，在玻璃管上所加的竖直向下的的拉力至少为多大？

参考答案：

本题解析：
状态1如图甲，状态2如图乙。
以气体为研究对象 由玻马定律

以玻璃管为研究对象
状态1：
状态2：

本题难度：简单

5、填空题  如图所示，在针管中封闭有一定质量的气体，当温度不变时，用力压活塞使气体的体积减小，则管内气体的压强______（选填“变大”或“变小”），按照气体分子热运动理论从微观上解释，这是因为：______．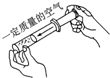

参考答案：气体温度不变，体积减小，由玻意耳定律可知，气体压强增大；
气体温度不变，分子平均动能不变，而分子的密集程度增大，
单位时间内对容器壁单位面积的碰撞次数增多，
器壁单位时间单位面积受到的压力变大，故压强增大．
故答案为：变大；分子密集程度增大．

本题解析：

本题难度：简单