1、计算题  如图所示是用导热性能良好的材料制成的气体实验装置，开始时封闭的空气柱长度为3 cm，此时气压表显示容器内压强p1＝1.0×105 Pa。求：
（1）将活塞缓慢向下推动，直到封闭空气柱长度变为2 cm时，气压表的示数是多少？
（2）将活塞快速向下推动，若在压缩气体过程中，气体内能增加了1.5 J，气体放出的热量为1.4 J，那么活塞对气体做的功是多少？

参考答案：解：（1）缓慢压缩时，气体温度不变，L0＝3 cm，L＝2 cm，p0＝1.0×105 Pa
设被压缩后气体压强为p，由玻意耳定律有：p0L0S＝pLS
解得：p＝1.5×105 Pa
（2）由热力学第一定律有：ΔU＝W＋Q
W＝ΔU－Q＝1.5－(－1.4)＝2.9 J

本题解析：

本题难度：一般

2、计算题  如图，在大气中有一水平放置的固定圆筒，它由a、b和c三个粗细不同的部分连接而成，各部分的横截而积分别为2S、1/2S和S。已知大气压强为p0，温度为T0。两活塞A和B用一根长为4l的不可伸长的轻线相连，把温度为T0的空气密封在两活塞之间，此时两活塞的位置如图所示现对被密封的气体加热，使其温度缓慢上升到T若活塞与圆筒壁之间的摩擦可忽略，此时两活塞之间气体的压强可能为多少？

参考答案：

解：设加热前，被密封气体的压强为P1，轻线的张力为f。
因两活塞都处在静止状态，对活塞A有2P0S -2p1S+f=0 ①
对活塞B有p1S-P0S-f=0 ②
由①②式得p1= P0③
?f=0 ④
即被密封气体的压强与大气压强相等，轻线处在拉直的松弛状态，
这时气体的体积V1= 2S1+S1+ S1=4S1 ⑤
对气体加热时，被密封气体温度缓慢升高，两活塞一起向左缓慢移动，气体体积增大，压强保持p1不变，若持续加热，此过程会一直持续到活塞向左移动的距离等于l为止，
这时气体的体积V1=4S1+S1=5S1⑥
设此时气体的温度为T2，由盖·吕萨克定律V2∝T2，即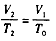⑦
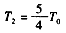由③⑤⑥⑦得⑧
由此可知，当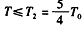时，气体的压强P2=P0⑨
当T>T2时，活塞已无法移动，被密封气体的体积保持V2不变，
气体经历一等容升压过程当气体的温度为T时，设其压强为p，由查理定律p∝T，即有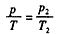⑩
即当时，气体的压强为。

本题解析：

本题难度：一般

3、选择题  如图所示，竖直放置的气缸内有一可作无摩擦滑动的活塞，活塞面积为2.0×10-3m2，活塞质量可忽略，气缸内封闭一定质量的气体，气体体积为V，温度是27℃，大气压强为1.0×105Pa。

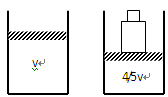
问：
（1）在活塞上放一个质量为多少kg的砝码，使气缸内气体的体积为原来体积的4/5；
（2）要使体积恢复到V，应使气体温度升高到多少摄氏度？

参考答案：（1）m＝0.5kg?（2）102℃

本题解析：（1）、P1＝P0＝1.0×105Pa?V1＝V? V2＝4V/5?……………….1分?
由玻意耳定律?P1V1＝P2V2?
P2＝1.25×105Pa＝P0＋mg/S?m＝0.5kg?……………….2分
（2）、气体为等压变化?由盖·吕萨克定律V1/T1＝V2/T2?……………….1分
T2＝375K t2＝102℃…?………….2分
点评：正确应用理想气体状态方程的前提是：判断此变化过程是属于等压、等容、还是等温变化．

本题难度：简单

4、选择题  一根均匀导线，现将它均匀拉长，使导线的直径减小为原来的一半，此时它的阻值为64 Ω．则导线原来的电阻值为
A.128 Ω
B.32 Ω
C.4 Ω
D.2 Ω

参考答案：C

本题解析：

本题难度：困难

5、简答题  如图甲所示，竖直放置的汽缸内壁光滑，活塞厚度与质量均不计，在B处设有限制装置，使活塞只能在B以上运动，B以下汽缸的容积为V0，A、B之间的容积为0.2V0．开始时活塞在A处，温度为87℃，大气压强为p0，现缓慢降低汽缸内气体的温度，直至活塞移动到A、B的正中间，然后保持温度不变，在活塞上缓慢加砂，直至活塞刚好移动到B，然后再缓慢降低汽缸内气体的温度，直到-3℃．求：
（1）活塞刚到达B处时的温度TB；
（2）缸内气体最后的压强p；
（3）在图乙中画出整个过程的p-V图线．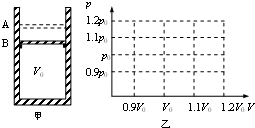

参考答案：

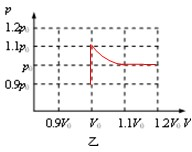
（1）缓慢降低汽缸内气体的温度，直至活塞移动到A、B的正中间，这个过程是等压过程：
根据盖吕萨克定律：VATA=VBTB
代入数据1.2V0360=1.1V0TB，
解得TB=330K，
然后保持温度不变，在活塞上缓慢加砂，直至活塞刚好移动到B，这个过程是等温过程，故活塞刚到达B处时的温度就为330K．
（2）保持温度不变，在活塞上缓慢加砂，直至活塞刚好移动到B，这个过程是等温过程：
根据玻意耳定律有：p0×1.1V0=p1×V0，
解得p1=1.1p0，
再接下是等容过程，根据查理定律有：1.1p0330=p270，
解得p=0.9p0
（3）整个过程的p-V图线，如右所示．
答：（1）活塞刚到达B处时的温度TB为330K；
（2）缸内气体最后的压强p为0.9p0；
（3）整个过程的p-V图线，如上所示．

本题解析：

本题难度：一般