1、计算题 (原创)(16分)某兴趣小组设计了一种实验装置,用来研究碰撞问题,其模型如图所示,光滑轨道中间部分水平,右侧为位于竖直平面内半径为R的半圆,在最低点与直轨道相切.5个大小相同、质量不等的小球并列静置于水平部分,球间有微小间隔,从左到右,球的编号依次为0、1、2、3、4,球的质量依次递减,每球质量与其相邻左球质量之比为k(k<1).将0号球向左拉至左侧轨道距水平高h处,然后由静止释放,使其与1号球碰撞,1号球再与2号球碰撞……所有碰撞皆为无机械能损失的正碰(不计空气阻力,小球可视为质点,重力加速度为g).
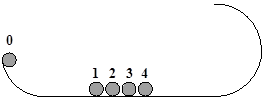
(1)0号球与1号球碰撞后,1号球的速度大小v1;
(2)若已知h=0.1m,R=0.64m,要使4号球碰撞后能过右侧轨道的最高点,问k值为多少?
参考答案:(1)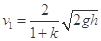 (2)
(2)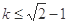
本题解析:(1)0号球碰前速度为v0,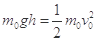 (2分)
(2分)
碰撞过程: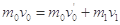 (2分)
(2分)
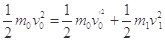 (2分)
(2分)
解得: (2分)
(2分)
(2)同理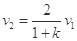
故: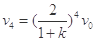 (2分)
(2分)
4号球从最低点到最高点: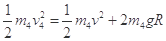 (2分)
(2分)
4号球在最高点: 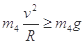 (2分)
(2分)
解得: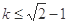 (2分)
(2分)
考点:本题考查了动量守恒定律、动能定理。
本题难度:困难
2、实验题 如图所示,质量为m、半径为R的小球,放在半径为2R、质量为2m的大空心球内.大球开始静止在光滑的水平面上,当小球从图示位置无初速度沿大球内壁滚到最低点时,大球移动的距离是___________.
参考答案:s=
本题解析:设大球运动的位移为s,由图3知小球运动的位移为(R-s)
由“人船模型”知两球在水平方向动量守恒,因此有 m(R-s)=2ms 解得:s=
本题难度:简单
3、计算题 (10分)如图所示,木板B的质量M="2" kg,与右墙距离为S.物体A(可视为质点)质量m="l" kg,以初速度v0="6" m/s从左端水平滑上B.己知A与B间的动摩擦因数μ=0.2,在B第一次撞墙前,A已经与B相对静止.地面光滑,B与两面墙的碰撞都是弹性的。求:
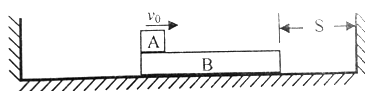
①S的最小值:
②若A始终未滑离B,A相对于B滑行的总路程是多少?
参考答案:2m? 9m
本题解析:①设B与挡板相碰时的速度大小为v1,
由动量守恒定律得mv0=(M+m)v1,(2分)
求出v1=2m/s.?(1分)
A与B刚好共速时B到达挡板S距离最短,对B用动能定理,
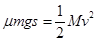 (2分)
(2分)
S的最小值为s= 2m(1分)
②经过足够多次的碰撞后,由于不断有摩擦力做功,最终AB速度都变为零,则在整个过程中,平板车和物块的动能都克服摩擦力做功转化为内能,因此有:
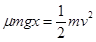 ?(3分)
?(3分)
x=9m?(1分)
本题难度:简单
4、简答题 如图所示,一质量M=1.0kg的砂摆,用轻绳悬于天花板上O点.另有一玩具枪能连续发射质量m=0.01kg,速度v=4.0m/s的小钢珠.现将砂摆拉离平衡位置,由高h=0.20m处无初速度释放,恰在砂摆向右摆到最低点时,玩具枪发射的第一颗小钢珠水平向左射入砂摆,二者在极短时间内达到共同速度.不计空气阻力,取g=10m/s2.
(1)求第一颗小钢珠射入砂摆前的瞬间,砂摆的速度大小v0;
(2)求第一颗小钢珠射入砂摆后的瞬间,砂摆的速度大小v1;
(3)第一颗小钢珠射入后,每当砂摆向左运动到最低点时,都有一颗同样的小钢珠水平向左射入砂摆,并留在砂摆中.当第n颗小钢珠射入后,砂摆能达到初始释放的高度h,求n.
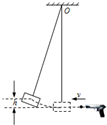
参考答案:(1)砂摆从释放到最低点,由动能定理:
Mgh=12Mv02-0,解得:v0=
本题解析:
本题难度:一般
5、选择题 A、B两球之间压缩一根轻弹簧,静置于光滑水平桌面上.已知A、B两球质量分别为2 m和m.当用板挡住A球而只释放B球时,B球被弹出落于距桌面水平距离为s的水平地面上,如图,问当用同样的程度压缩弹簧,取走A左边的挡板,将A、B同时释放,B球的落地点距桌面距离为(?)
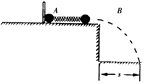
A. ? B.
? B.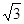 s? C.s? D.
s? C.s? D.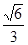 s
s
参考答案:D
本题解析:考点:
专题:动量与动能定理或能的转化与守恒定律综合.
分析:A、B两球之间压缩一根轻弹簧,当用板挡住A球而只释放B球时,弹性势能完全转化为B球的动能,以一定的初速度抛出,借助于抛出水平位移可确定弹簧的弹性势能.当用同样的程度压缩弹簧,取走A左边的挡板,将A、B同时释放,由动量守恒定律与机械能守恒定律可求出B球获得的速度,再由平抛运动规律可算出抛出的水平位移.
解答:解:当用板挡住A球而只释放B球时,B球做平抛运动.设高度为h,则有vB=s ,所以弹性势能为E=
,所以弹性势能为E=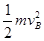 =
=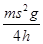 当用同样的程度压缩弹簧,取走A左边的挡板,将A、B同时释放,由动量守恒定律可得:0=2mvA-mvB?所以vA:vB=1:2.因此A球与B球获得的动能之比EkA:EkB=1:2.所以B球的获得动能为:
当用同样的程度压缩弹簧,取走A左边的挡板,将A、B同时释放,由动量守恒定律可得:0=2mvA-mvB?所以vA:vB=1:2.因此A球与B球获得的动能之比EkA:EkB=1:2.所以B球的获得动能为: .
.
那么B球抛出初速度为vB=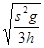 ,则平抛后落地水平位移为
,则平抛后落地水平位移为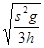
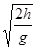 =
=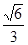 s
s
故选:D
点评:考查动量守恒定律、机械能守恒定律,及平抛运动规律.两种情况下,弹性势能完全相同.在弹簧恢复过程中弹性势能转化为动能.
本题难度:一般