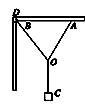
1、选择题  三段等长的、不可伸长的细线结于O点，A端固定在水平杆上，B端接在套在竖直光滑杆上的轻圆环上，C端挂一重物，重物质量为m；开始时轻圆环固定在紧靠D端的位置，AD等于绳长OA，静止时如图所示．今不再固定圆环，让圆环可以在竖直光滑杆上自由滑动，再次静止时OA绳拉力为FTA，OB绳拉力为FTB，则? (　　)

A．FTA<mg，FTB>mg
B．FTA＝mg，FTB＝0
C．FTA＝mg，FTB＝mg
D．FTA>mg，FTB＝mg

参考答案：B

本题解析：略

本题难度：一般

2、计算题   如图所示放在水平地面上的物体P的重量为GP=10N，与P相连的细线通过光滑的滑轮挂了一个重物Q拉住物体P，重物Q的重量为GQ=2N，此时两物体保持静止状态，线与水平方向成30?角，则物体P受到地面对它的摩擦力F1与地面对它的支持力F2多大？

参考答案：

本题解析：
首先对Q进行受力分析如图示：

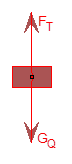
对Q由平衡条件可知：FT=GQ------------------------①
对P受力分析如图示：

建立如图所示的直角坐标系，将FT正交分解得
在x轴上由平衡条件，有：-------------②
在y轴上由平衡条件，有：----③
联立①②③得：

本题难度：简单

3、简答题  如图所示，AB和CD是足够长的平行光滑导轨，其间距为l，导轨平面与水平面的夹角为θ，整个装置处在磁感应强度为B、方向垂直于导轨平面上的匀强磁场中，AC端连有电阻值为R的电阻．若将一质量为M，垂直于导轨的金属棒EF在距BD端s处由静止释放，在EF棒滑至低端前会有加速和匀速两个运动阶段，今用大小为F、方向沿斜面向上的恒力把EF棒从BD位置由静止推至距BD端s处，突然撤去恒力F，棒EF最后又回到BD端，（金属棒、导轨的电阻均不计）求：
（1）EF棒下滑过程中的最大速度；
（2）EF棒自BD端出发又回到BD端的整个过程中，有多少电能转化成了内能？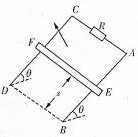

参考答案：（1）如图，当EF棒从距BD端s处由静止开始滑至BD的过程中，受力情况如图所示，棒所受的安培力为


? F安=BIl=B2l2vR
根据牛顿第二定律得
? a=Mgsinθ-B2l2vRM? ①
所以，EF棒由静止开始做加速度减小的加速运动，当a=0时做匀速运动，速度达到最大值vm，由①式a=0有，Mgsinθ=B2l2vmR
得，vm=MgRsinθB2l2
（2）由恒力推到距BD端s处后，棒先减速到零，然后从静止下滑，当加速度减至零时，在滑回BD之前已达到最大，开始匀速运动．根据能量守恒定律得
? Fs-Q=12Mv2m
解得，Q=Fs-12M(MgRsinθB2l2)2
答：（1）EF棒下滑过程中的最大速度是MgRsinθB2l2；
（2）EF棒自BD端出发又回到BD端的整个过程中，有Fs-12M(MgRsinθB2l2)2电能转化成了内能．

本题解析：

本题难度：一般

4、计算题  如图所示，轻绳OA一端系于天花板上，与竖直方向的夹角为30°，水平轻绳OB的一端系于竖直墙上，O点挂一重物．如果绳OA能承受最大拉力是300N，求

小题1:在O点最多能挂多重的重物?
小题2:此时绳OB的拉力是多大?

参考答案：
【小题1150√3N
小题2:150N

本题解析：本题考查力的合成与分解。根据受力平衡可知三拉力合力为0，则绳OA拉力沿竖直方向的分量等于物体重力，水平分量等于OB绳上拉力。则。

本题难度：简单

5、选择题 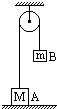 两个物体A和B，质量分别为M和m，用跨过定滑轮的轻绳相连，A静止于水平地面上，如图所示．不计摩擦，A对绳的作用力的大小与地面对A的作用力的大小分别为
A.mg，（M-m）g
B.mg，Mg
C.（M-m）g，Mg
D.（M+m）g，（M-m）g

参考答案：A

本题解析：分析：由物体B静止，求出绳子的拉力．以A为研究对象，根据平衡条件求出地面对A的作用力的大小．
解答：以B为研究对象，绳子的拉力F=mg．
? 再以A为研究对象，得到F+FN=Mg，得到FN=Mg-F=（M-m）g
故选A
点评：本题采用的是隔离法．当物体处于平衡状态时，采用隔离都可以求解．当几个物体都处于平衡状态时，也可以采用整体法．

本题难度：简单