1、计算题 竖直运行的升降机地板上有一个质量为100kg的物体,它对地板的压力随时间变化的图像如图所示。若升降机从静止开始向上运动,g取10m/s2,求8s内升降机上升的高度?

参考答案:解:取升降机地板上的物体为研究对象,物体受力情况如图所示。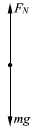
取向上为正方向。由牛顿第三定律可知,物体对地面的压力等于地面对物体的支持力,即F=FN。
在0~2s内,FN1=F1>mg,物体所受合外力竖直向上,所以物体向上做匀加速直线运动。
由牛顿第二定律得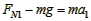 ①?
①?
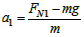
?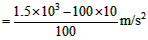
? 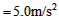 ? ②
? ②
所以物体的位移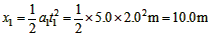
物体2s末的速度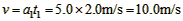 ③
③
在2~6s内,FN2=mg,物体所受合外力为零,所以物体向上做匀速直线运动,
则物体的位移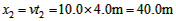 ④
④
在6~8s内,FN3<mg
物体所受合外力方向竖直向下,所以物体向上做匀减速直线运动,初速度为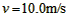 。
。
由牛顿第二定律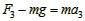 ⑤
⑤
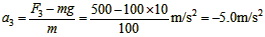
所以物体的位移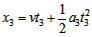
? 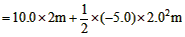 ?
?
? 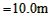 ⑥
⑥
所整个过程中物体位移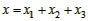
? 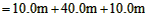 ?
?
? 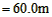 ⑦
⑦
本题解析:
本题难度:困难
2、选择题 一人自街上路灯的正下方经过,看到自己头部的影子正好在自己脚下,如果人以不变的速度沿直线朝前走,则他自己头部的影子相对于地面的运动情况是
A.匀速直线运动
B.匀加速直线运动
C.变加速直线运动
D.曲线运动
参考答案:A
本题解析:
根据光的直线传播规律作出几何图形,确定任意时刻人头影的位置,应用运动学公式和几何知识推导出人头影的位移或速度随时间的变化关系即可判定.设灯高SO=H,人高AO=h,如图所示,

人以速度v经任意时间t到达A1′位置处,由光的直线传播知人头A1的影子应在图示O′处,由相似三角形的比例关系可得: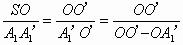 .其中SO=H,A1A1′=AO=h,OO′为人头影在t时间内的位移,OA1′=vt代入上式得
.其中SO=H,A1A1′=AO=h,OO′为人头影在t时间内的位移,OA1′=vt代入上式得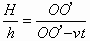 解得:
解得: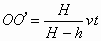 .因为H、h、v是恒量,所以人头影子的位移OO′跟时间t成正比,即人头影子做匀速运动.
.因为H、h、v是恒量,所以人头影子的位移OO′跟时间t成正比,即人头影子做匀速运动.
从运动学角度判定物体做什么运动一般可先求出物体(或某点)的位移随时间的变化关系式,根据位移与时间是一个一次函数还是二次函数等即可判断物体做什么运动.切勿凭感觉乱猜.
本题难度:简单
3、计算题 (8分)如图所示,质量m=6kg的物块静止在水平桌面上,受到与水平方向成θ=37°角的作用力F。(sin37°=0.6 cos37°=0.8 g=10m/s2)
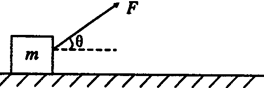
(1)F=20N时,物块恰好沿水平面向右做匀速直线运动,求物块与水平桌面的动摩擦因数μ?(保留两位有效数字)
(2)若保持以上动摩擦因数不变,当力F=40N时物体由静止开始运动,求3s内物体的位移大小?
参考答案: ?
?
本题解析:解:(1)物体受力情况如图所示,根据受力平衡,有:
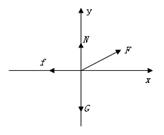
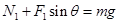 ①
①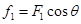 ?
? ?②
?②
代入数据,解得: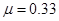 ?(4分)
?(4分)
(2)根据题意有:  ?③?
?③?
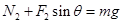 ?
? ?④
?④
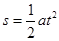 ?⑤?
?⑤?
代入数据,解③④⑤式得:物体的位移大小:?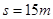 (4分)
(4分)
本题难度:一般
4、简答题 如图所示,光滑斜面倾角为30°,水平面粗糙摩擦系数为μ,现将A、B两物体(可视为质点)同时由静止释放,两物体初始位置距斜面底端O的距离为LA=L,LB=4L.不考虑两物体在转折O处的能量损失.求:
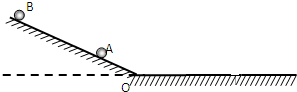
(1)两物体滑上水平面的时间差?
(2)若摩擦系数μ>
,当B物滑上水平面后,追上A物所用的时间?
(3)若摩擦系数μ=,当B物滑上水平面后,追上A物所用的时间?
参考答案:(1)根据受力分析知物体的加速度为:a=gsinθ=12g
tA=
本题解析:
本题难度:一般
5、简答题 以5米/秒匀速上升的气球,当升到20米高时,从气球上落下一小球,小球的质量为500克,小球在运动过程中遇到的阻力是0.1牛,求经过多长时间到达地面
参考答案:2.6秒
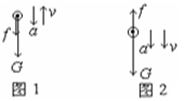
本题解析:小球在离开气球前,随气球一起向上做匀速直线运动。离开气球后,由于重力和阻力的作用,小球做匀减速直线运动上升,其初速度为5米/秒,其加速度由于重力和阻力二力之和而产生(如图1)
小球达到最高点后,将做初速度为零的匀加速运动下落,其加速度由于重力和阻力二力之差而产生(如图2)根据牛顿第二定律,小球在上升过程中有:?
mg + f=ma1, --(1分)
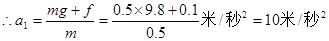 ?
?
 ?(1分)
?(1分)
再由运动公式得上升高度及上升时间:
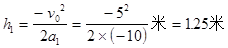 ?(1分)
?(1分)
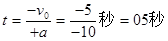 ?(1分)
?(1分)
(以上两式以向上为正,a向下,所以a=-10米/秒2,h为正,说明h1向上)
小球从最高点下落的过程中,由牛顿第二定律得
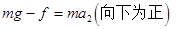 ?(1分)
?(1分)
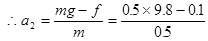
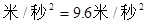 ?(1分)
?(1分)
又由于下落高度h2=h1+H0=1.25米+20米=21.25米,再由运动学公式得?
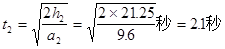 ?(1分)
?(1分)
所以小球从离开气球到到达地面所用时间秒t=t1+t2=2.6秒。?(1分)
本题难度:简单