1、计算题  （15分）如图所示，是某公园设计的一种惊险刺激的娱乐设施，轨道CD部分粗糙，μ=0.1，其余均光滑。第一个圆管轨道的半径R=4m，第二个圆管轨道的半径r=3.6m。一挑战者质量m=60kg，沿斜面轨道滑下，滑入第一个圆管形轨道（假设转折处无能量损失），挑战者到达A、B两处最高点时刚好对管壁无压力，然后从平台上飞入水池内，水面离轨道的距离h=1m。g取10 m/s2，管的内径忽略不计，人可视为质点。

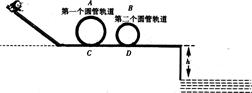
求：（1）挑战者若能完成上述过程，则他应从离水平轨道多高的地方开始下滑?（2）CD部分的长度是多少?（3）挑战者入水时速度的大小和方向?

参考答案：⑴ 10m?⑵64m?⑶ 16?m/s 与水面的夹角θ=arctan5/8

本题解析：（1）（4分）在A点无压力，则 mg=mvA2/R?（1分）
设从离水平轨道高为H处开始下滑，从静止开始到A由动能定理得
mgH=mg·2R+ mvA2/2?（2分）解得H=10m?（1分）
（2）（7分）从开始下滑到C点，由动能定理得mgH=mvC2/2?（1分）
在B点无压力，则 mg=mvB2/r?（1分）
从D点到B点，由动能定理得mvD2/2=mg·2r+ mvB2/2?（2分）
从C点到D点，由动能定理得-μmgSCD=mvD2/2- mvC2/2?（2分）
解得 SCD=64m?（1分）
（3）（5分）设落水点为E，落水时，竖直方向vy2=2gh?（1分）
解得 vy="10m/s" （1分）
水平方向速度大小为vD不变。
解得得vE≈16?m/s。（1分）
设方向与水面成θ，所以tanθ=vy/vD=5/8。?（1分）
解得θ=arctan5/8?（1分）

本题难度：简单

2、计算题  如图所示，质量为m的物体，从高h，倾角为θ的光滑斜面顶端由静止开始下滑，最后停在水平面上。已知物体与水平面的动摩擦因数为μ。求：

（1）?物体滑至斜面底端时的速度大小；
（2）?物体在水平面上滑过的距离。

参考答案：（1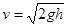）（2）

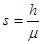
本题解析：（1）物体由斜面下滑到底端的过程，由动能定理得
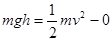?①所以，物体滑至斜面底端时的速度为：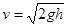
（2）设物体在水平面上滑过的距离为s，则物体在水平面运动的过程，取运动方向为正方向，由动能定理得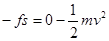：?②滑动摩擦力的大小：?③
由①②③得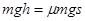：，所以：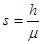
（2）另解：设物体在水平面上滑过的距离为s，则物体运动的全过程，
由动能定理得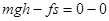：?①滑动摩擦力的大小：?②
由①②得：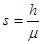
本题考查动能定理的应用，从最高点运动到最低点过程中只有重力做功，由此先求得到达最低点速度大小，物体在平面上滑动过程中只有滑动摩擦力做功，由动能定理可求得动摩擦因数大小

本题难度：一般

3、填空题  如图所示，一半径为R的光滑圆环，竖直放在水平向右的匀强电场中，匀强电场的电场强度大小为E．环上a、c是竖直直径的两端，b、d是水平直径的两端，质量为m的带电小球套在圆环上，并可沿环无摩擦滑动，已知小球自a点由静止释放，沿abc运动到d点时速度恰好为零，由此可知小球所受重力______（选填“大于”、“小于”或“等于”）带电小球所受的静电力．小球在______（选填“a”、“b”、“c”或“d”）点时的电势能最小．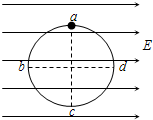

参考答案：根据动能定理，合力做的功等于动能的增加量；
从a到d过程，有：mg?R-qE?R=0
解得? qE=mg
即电场力与重力大小相等，
根据功能关系，电场力做正功，电势能减小，电场力向左，故运动到b点时电场力做的功最多，
所以电势能减小的最多，即小球在b点时的电势能最小．
故答案为：等于? b

本题解析：

本题难度：一般

4、计算题  运动员驾驶摩托车做腾跃特技表演是一种刺激性很强的运动项目。如下图所示，运动员驾驶摩托车的在AB段加速，到B点时速度为v0＝20m/s，之后以恒定功率P＝1.8kw冲上曲面BCDE，经t＝13s的时间到达E点时，关闭发动机后水平飞出。已知人和车的总质量m＝180 kg，坡顶高度h＝5m，落地点与E点的水平距离x＝16m，重力加速度g＝10m/s2。求摩托车在冲上坡顶的过程中克服阻力做的功。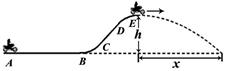

参考答案：27360J

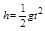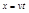本题解析：对摩托车的平抛运动过程，有（2分）
（2分）
摩托车在斜坡上运动时，由动能定理得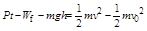?（2分）
联立解得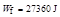?（2分）

本题难度：一般

5、计算题  质量为m=1kg的物体与水平面间的动摩擦因数μ=0.6，在F=10N水平拉力作用下，由静止开始前进x1=2m后撤去外力， g=10m/s2,求：
（1）撤去外力时物体速度多大？
（2）撤去外力后还能运动多远？

参考答案：（1）Fx1-fx1=?(3分)? f=μmg? (1分)
解得v="4m/s?" （1分）
(2)Fx1-f(x1+x2)="0?" （4分）?解得x2="1.3m?" （1分）

本题解析：略

本题难度：简单