1、简答题  甲、乙两车同时经过某路口同方向做直线运动，甲以15m/s的速度做匀速运动，乙从此路口由静止开始以3m/s2的加速度做匀加速直线运动．问：
（1）从它们经过路口开始计时多长时间后，它们第一次相遇？相遇时距路口多远？
（2）在相遇前两物体何时距离最大？最大距离是多少？

参考答案：（1）设经t?1时间第一次相遇，有s?甲=vt?1，s?乙=12at21，s?甲=s?乙，解得t?1=10s，s?甲=150m
即它们经10s后相遇，相遇时距路口150m．
（2）相遇前当两物体速度相等时距离最大，设时间是t?2，有v=at?2，解得t?2=5s
所以△s=vt?2-12at22，代入数据得△s=27.5m
即相遇前5s时距离最大，最大距离是27.5m．

本题解析：

本题难度：一般

2、选择题  在德国首都柏林举行的世界田径锦标赛女子跳高决赛中，克罗地亚选手弗拉希奇以2.04m的成绩获得冠军。弗拉希奇身高约为1.93 m，忽略空气阻力，g取10 m/s2。则下列说法正确的是

A．弗拉希奇下降过程处于失重状态
B．弗拉希奇起跳以后在上升过程处于超重状态
C．弗拉希奇起跳时地面对她的支持力等于她所受的重力
D．弗拉希奇起跳时的初速度大约为3 m/s

参考答案：A

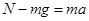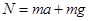本题解析：运动员起跳后上升过程做减速运动，下降过程做加速运动，加速度都是向下，所以运动员在这两个过程中整体处于失重状态，A正确B错误；起跳时加速度向上，根据牛顿第二定律可得，即，所以地面对她的支持力大于重力故能顺利起跳，C错误；运动员起跳时重心在腰部，背越式过杆，重心上升高度可按1m估算，则起跳时的初速度约为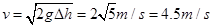，D错误。

本题难度：一般

3、计算题  如图所示，质量m＝1 kg的球穿在斜杆上，斜杆与水平方向成α＝30°角，球与杆之间的动摩擦因数μ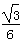＝，球受到竖直向上的拉力F＝20 N．则球的加速度为多少？(g取10 m/s2)

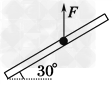
参考答案：解：球受重力G、杆的支持力FN、杆的摩擦力Ff和竖直向上的拉力四个力的作用(如图所示)，建立直角坐标系，则由牛顿第二定律得

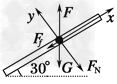
Fsin30°－Gsin30°－Ff＝ma
Fcos30°－Gcos30°－FN＝0
Ff＝μFN
联立以上各式即可解得a＝2.5 m/s2.

本题解析：

本题难度：一般

4、选择题  关于牛顿第二定律F=ma，下列说法正确的是（　　）
A．a的方向与F的方向相同
B．a的方向与F的方向相反
C．a的方向与F的方向无关
D．a的方向与F的方向垂直

参考答案：根据牛顿第二定律F=ma得：
a=Fm
质量是标量，力和加速度都是矢量，所以加速度方向与合外力方向相同．
故选A

本题解析：

本题难度：一般

5、选择题  汽车从平直公路驶上一斜坡，牵引力逐渐增大而输出功率保持不变，则在此过程中的初始阶段，汽车的
A.加速度逐渐减小，速度逐渐减小
B.加速度逐渐增大，速度逐渐增大
C加速度逐渐增大，速度逐渐减小
D 加速度逐渐减小，速度逐渐增大

参考答案：A

本题解析：
试题分析: 由P=F?v可知，功率不变，汽车的牵引力逐渐增大，其上坡的速度逐渐减小，汽车的加速度方向沿坡向下，对汽车进行受力分析：汽车受到重力、牵引力、阻力Ff．设斜坡与水平面的夹角为θ，由牛顿第二定律得：mgsinθ+Ff-F=ma，随F增大，a逐渐减小，综上所述，加速度逐渐减小，速度逐渐减小，故A正确，B、C、D错误．

本题难度：一般