1、计算题 质量为2 kg的物体放到水平地板上,用一轻弹簧水平拉该物体,物体由静止开始,开始 2 s 时间内,物体运动 2 m 位移,此过程中弹簧始终保持伸长3 cm,己知弹簧的劲度系数为 k ="100" N/m.求:物体和地板间的动摩擦因数.
参考答案:
本题解析:运动过程中的加速度?
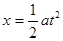

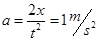

弹簧拉力
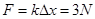
由牛顿第二定律

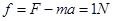
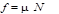
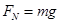

本题难度:简单
2、简答题 如图所示,两木板A、B并排放在地面上,A左端放一小滑块,滑块在F=6N的水平力作用下由静止开始向右运动.已知木板A、B长度均为l=1m,木板A的质量MA=3kg,小滑块及木板B的质量均为m=1kg,小滑块与木板A、B间的动摩擦因数均为μ1=0.4,木板A、B与地面间的动摩擦因数均为μ2=0.1,重力加速度g=10m/s2.求:
(1)小滑块在木板A上运动的时间;
(2)木板B获得的最大速度.

参考答案:(1)小滑块对木板A的摩擦力:
f1=μ1mg=0.4×1×10=4N
木板A与B整体受到地面的最大静摩擦力:
f2=μ2(2m+MA)g=0.1×(2×1+3)=5N
f1<f2,小滑块滑上木板A后,木板A保持静止
设小滑块滑动的加速度为a1,则:
F-μ1mg=ma1
根据运动学公式,有:
l=12a1t21
解得:
t1=1s
(2)设小滑块滑上B时,小滑块速度v1,B的加速度a2,经过时间t2滑块与B速度脱离,滑块的位移x块,B的位移xB,B的最大速度v2,则:
μ1mg-2μ2mg=ma2
vB=a2t2
xB=12a2t22
v1=a1t1
x块=v1t2+12a1t22
x块-xB=l
联立解得:vB=1m/s
答:(1)小滑块在木板A上运动的时间为1s;(2)木板B获得的最大速度为1m/s.
本题解析:
本题难度:一般
3、选择题 如图两个内壁光滑、半径不同的半球形碗,放在不同高度的水平面上,使两碗口处于同一水平面.现将质量相同的两个带等量负电荷的小球(小球半径远小于碗的半径),分别从两个碗的边缘由静止释放,当两球分别沿圆弧通过碗的最低点时(? )

A.不加电场时,两小球的速度大小相等,若加向上的匀强电场时,速度大小仍相等.
B.不加电场时,两小球的机械能大小相等,若加向上的匀强电场时,机械能大小仍相等.
C.不加电场时,两小球对碗底的压力大小相等,若在球心处加一相同的点电荷,压力大小不再相等.
D.不加电场时,两小球对碗底的压力大小相等,若加向上的匀强电场时,压力仍大小相等.
参考答案:CD
本题解析:当不加电场时,小球从图示位置到最低点的过程中机械能守恒,取初位置所在平面为零势能面,则有根据动能定理:mgh=mgR=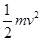 ,
, 两球下落高度不同,则通过碗的最低点速度大小不相等,A错误;只有重力做功的情况下,机械能守恒,若加向上的匀强电场时,电场力做功,机械能会变化,B错误;不加电场时,在最低点
两球下落高度不同,则通过碗的最低点速度大小不相等,A错误;只有重力做功的情况下,机械能守恒,若加向上的匀强电场时,电场力做功,机械能会变化,B错误;不加电场时,在最低点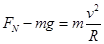 得
得 ,两球对碗底的压力大小相等,若在球心处加一相同的点电荷,两小球都在点电荷的等势面上运动,电场力不做功,机械能仍守恒,在最低点F=3mg-F库,F库不同,故两球对碗的压力不等.故C正确,D错误。
,两球对碗底的压力大小相等,若在球心处加一相同的点电荷,两小球都在点电荷的等势面上运动,电场力不做功,机械能仍守恒,在最低点F=3mg-F库,F库不同,故两球对碗的压力不等.故C正确,D错误。
本题难度:一般
4、简答题 如图所示,一个厚度不计的圆环A,紧套在长度为L的圆柱体B的上端,A、B两者的质量均为m,A与B之间的最大静摩擦力与滑动摩擦力相同,其大小为kmg(k>1).B在离地H高处由静止开始落下,触地后能竖直向上弹起,触地时间极短,且无动能损失,B与地碰撞若干次后A与B分离.求:
(1)B与地第一次碰撞后,经多长时间A与B达到相同的速度;
(2)当A与B第一次达到相同速度时,B下端离地面的高度是多少.

参考答案:物体A、B一起下落H过程,机械能守恒得:
2mgH=12×2mv2
解得v=
本题解析:
本题难度:一般
5、填空题 力的合成与分解用到的主要科学方法是______,验证牛顿第二定律实验中先保持小车的质量不变,改变所挂钩码的质量,测定相应的加速度,再保持钩码的质量不变,改变小车的质量,测定相应的加速度,这用的科学方法是______.
参考答案:力的合成与分解用到的主要科学方法是等效替代,
验证牛顿第二定律实验中先保持小车的质量不变,改变所挂钩码的质量,测定相应的加速度,再保持钩码的质量不变,改变小车的质量,测定相应的加速度,这用的科学方法是控制变量.
故答案为:等效替代,控制变量.
本题解析:
本题难度:简单