1、计算题  已知地球半径为6400km ，已知太阳向空间辐射太阳能的总功率为3.8 ×1026W ，辐射到地球上的太 阳能总功率为1.7 ×1017W.
(1)估算地球到太阳的距离;
(2)并计算太阳的质量．（G=6. 67 ×10-11 N ·m2/kg2 ）

参考答案：解：(1)设地球到太阳的距离为R ，
由能量分配可得，辐射到地球上的太阳能E=E 1·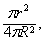
因 E1 =P1·t?E=P·t
且P1 = 3. 8×1026W,
P=1.7×107W,
所以=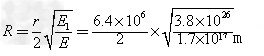
(2)已知地球绕太阳公转的周期为T=365×24×3600 s=3.15×107s.
由万有引力定律，得

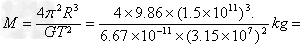
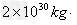
本题解析：

本题难度：一般

2、选择题  以下说法中正确的是（　　）
A．气体的温度越高，分子的平均动能越大
B．即使气体的温度很高，仍有一些分子的运动速度是非常小的
C．如果气体分子间的相互作用力小到可以忽略不计，则气体的内能只与温度有关
D．从单一热源吸取热量使之全部变成有用的机械功是不可能的

参考答案：AB

本题解析：

本题难度：一般

3、选择题  
(1)(4分) 下列说法正确的是            (填入正确选项前的字母。选对得4分，选不全得2分，错选或多选得0分)。
A．物体的内能是物体所有分子热运动的动能和分子间的势能之和
B．布朗运 动就是液体分子或者气体分子的热运动
C．利用浅层海水和深层海水之间的温度差制造一种热机，将海水的一部分内能转化为机械能是可能的
D．气体分子间距离减小时，分子间斥力增大，引力减小
E．一定量的理想气体，在压强不变时，分子每秒对器壁单位面积平均碰撞次数随着温度降低而增加
(2)(8分) 如图，粗细均匀的弯曲玻璃管A、B两端开口，管内有一段水银柱，中管内水银面与管口A之间气体柱长为lA＝40cm，右管内气体柱长为lB＝39cm。先将口B封闭，再将左管竖直插入水银槽中，设被封闭的气体为理想气体，整个过程温度不变，若稳定后进入左管的水银面比水银槽水银面低４cm，已知大气压强p0＝76cmHg，求：

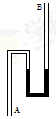
（i）A端上方气柱长度；
（ii）稳定后右管内的气体压强。

参考答案：（1）ACE；（2）（i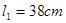）；（ii）78cmHg；

本题解析：（1）物体的内能是物体所有分子热运动的动能和分子间的势能之和，A正确；布朗运动是液体分子无规则热运动的反应；浅层海水和深层海水之间的温度差，就会有能量的转移和传递，可以通过热机将海水的一部分内能转化为机械能，C正确；气体分子间距离减小时，分子间斥力和引力都增大，D错误；压强是分子对器壁的碰撞而产生的，温度降低时，分子平均动能减小，压强不变时，分子每秒对器壁单位面积平均碰撞次数随着温度降低而增加，E正确。
(2)设A端上方气柱长度为l1，由题可知，插入水银槽后左管内气体压强为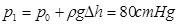  ①
由玻意耳定律得：     ②
所以A端上方气柱长度为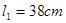   ③
（2）设右管水银面上升h，则右管内气柱长度为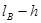，气体压强为 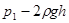  ④
由玻意耳定律得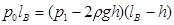：     ⑤
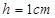解得       ⑥
所以右管内气体压强为             ⑦
评分标准：第一问3分；第二问5分。
①②③④⑥⑦每式1分，⑤每式2分
考点：分子动理论、理想气体状态方程

本题难度：一般

4、简答题  研究动能和势能转化规律的实验装置如图所示．
（1）关于实验下列做法中正确的是______（单选）
A．摆锤释放器在每次释放后都要调整高度
B．光电门传感器始终放在最低点
C．每次要用测平器使光电传感器的红外发射孔
对应于所要求高度的水平线
D．摆锤线长应调整到使摆线在摆动时能通过光电孔
（2）以摆锤所在位置的高度h为横坐标，摆锤速度v2/2为纵坐标，作出的图线应是图中的______（单选），图线的斜率大小表示______．

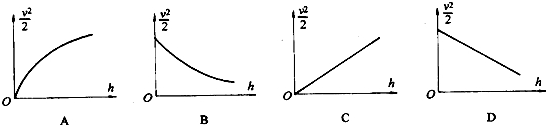
参考答案：（1）A．摆锤释放器在每次释放后不需要调整高度，故A错误．
B．光电门传感器不一定放在最低点，也可以在其他位置测量，故B错误．
C．每次要用测平器使光电传感器的红外发射孔对应于所要求高度的水平线，故C正确．
D．摆锤线长应调整到使摆锤在摆动时能通过光电孔，故D错误．
故选C．
（2）利用v2-h图线处理数据，如果mg（h0-h）=12mv2
作出的图线应是图中的D，那么12v2-h图线的斜率就等于g．
故答案为：（1）C?（2）D?（3）重力加速度g大小

本题解析：

本题难度：一般

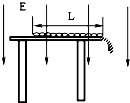
5、简答题  如图所示，有一柔软链条全长为L=1.0m，质量均匀分布，总质量为M=2.0kg．整条链条均匀带电，总带电量Q=1.0×10-6C，将链条放在离地足够高的水平桌面上．仅在水平桌面的上方存在匀强电场，电场强度E=2.0×107V/m．若桌面与链条之间的动摩擦因数为μ=0.5（重力加速度取g=10m/s2）．试求：
（1）当桌面下的链条多长时，桌面下的链条所受到的重力恰好等于链条受到的滑动摩擦力．
（2）链条从桌面上全部滑下所需的最小初动能．

参考答案：（1）设桌面下的链条长为x，链条质量分布均匀，所以在桌面下的链条的质量为xML，则有：
xMLg=μL-xL（Mg+QE），解得x=0.5 m；
（2）链条下滑0.5 m后就会自动下滑，此时速度正好为零时所需初动能最小，根据动能定理有：
12Mg×L4-Wf=0-Ek0，
由于f和N成正比，N和链条下滑的长度成正比，所以f是均匀变化的．
可以根据平均摩擦力来求Wf
Wf=f1+f22?L2
f1是最初瞬间的摩擦力，即fMAX，所以f1=20N
f2是下滑0.5m时的摩擦力，由第二问得知，其大小等于半根链条的重力，f2=10N
解得：Ek0=Wf-MgL8=f1+f28×L2-MgL8=7.5-2.5J=5J．
答：（1）当桌面下的链条0.5m时，桌面下的链条所受到的重力恰好等于链条受到的滑动摩擦力；
（2）从桌面上滑下全部链条所需的最小初动能为5J．

本题解析：

本题难度：一般