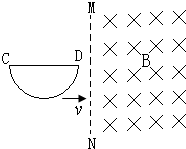
1、计算题 如下图1所示,水平面内的直角坐标系的第一象限有磁场分布,方向垂直于水平面向下,磁感应强度沿y轴方向没有变化,与横坐标x的关系如下图2所示,图线是双曲线(坐标轴是渐进线);顶角θ=45°的光滑金属长导轨 MON固定在水平面内,ON与x轴重合,一根与ON垂直的长导体棒在水平向右的外力作用下沿导轨MON向右滑动,导体棒在滑动过程中始终保持与导轨良好接触。已知t=0时,导体棒位于顶角O处;导体棒的质量为m=2kg;OM、ON接触处O点的接触电阻为R=0.5Ω,其余电阻不计;回路电动势E与时间t的关系如图3所示,图线是过原点的直线。求:
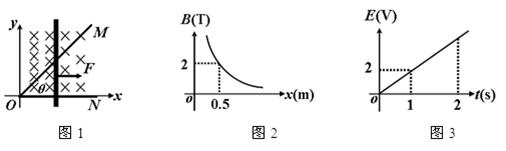
(1)t=2s时流过导体棒的电流强度I2的大小;
(2)1~2s时间内回路中流过的电量q的大小;
(3)导体棒滑动过程中水平外力F(单位:N)与横坐标x(单位:m)的关系式。
参考答案:(1)8A?(2) 6C?(3) 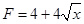
本题解析:(1)根据E—t图像中的图线是过原点的直线特点
有: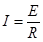 ?得:
?得: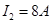 ?(2分)
?(2分)
(2)可判断I—t图像中的图线也是过原点的直线?(1分)
有:t=1s时 ?可有:
?可有: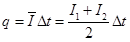 ?(2分)
?(2分)
得: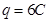 ?(1分)
?(1分)
(3)因θ=45°,可知任意t时刻回路中导体棒有效切割长度L=x?(2分)
再根据B—x图像中的图线是双曲线特点:Bx=1
有: 且
且 ?(2分)
?(2分)
可得: ,所以导体棒的运动是匀加速直线运动,加速度
,所以导体棒的运动是匀加速直线运动,加速度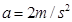 ?(2分)
?(2分)
又有: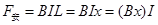 且
且 也与时间成正比?(2分)
也与时间成正比?(2分)
再有: ?(2分)
?(2分)
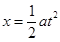 ?(2分)
?(2分)
得: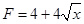 ?(2分)
?(2分)
本题难度:一般
2、计算题 在磁感应强度B=0.5T的匀强磁场中有一个正方形金属线圈abcd,边长L=0.2m。线圈的ad边与磁场的左侧边界重合,如图12-14所示,线圈的电阻R=0.4Ω.用外力把线圈从磁场中移出有两种方法:一种是用外力把线圈从左侧边界匀速平移出磁场;另一种是以ad边为轴,用力使线圈匀速转动移出磁场,两种过程所用时间都是t=0.1s。求

(1)线圈匀速平移出磁场的过程中,外力对线圈所做的功。
(2)线圈匀速转动移出磁场的过程中,外力对线圈所做的功。
参考答案:(1)0.01J? (2)0.012J
本题解析:(1)使线圈匀速平动移出磁场时,bc边切割磁感线而产生恒定感应电动势E=BLv.而v=L/t.?
外力对线圈做的功等于线圈中消耗的电能,即
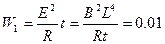 J?
J?
(2)线圈以ad边为轴匀速转出磁场时,线圈中产生的感应电动势和感应电流都是按正弦规律变化的,感应电动势和感应电流的最大值为: ?
?
外力对线圈做的功等于线圈中消耗的电能,即
 J
J
本题难度:一般
3、计算题 (12分)如图甲所示,一个圆形线圈匝数n = 1000匝、面积S = 2×10-2m2、电阻r =1Ω。在线圈外接一阻值为R = 4Ω的电阻。把线圈放入一个匀强磁场中,磁场方向垂直线圈平面向里,磁场的磁感强度B随时间变化规律如图乙所示。求:
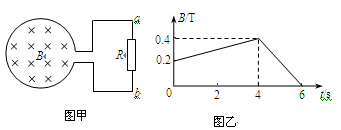
(1)0 ~ 4s内,回路中的感应电动势;
(2)t = 5s时,a、b两点哪点电势高;
(3)t = 5s时,电阻两端的电压U 。
参考答案:(1)1V;(2)a点的电势高于b点;(3)3.2V。
本题解析:(1)根据法拉第电磁感应定律得,0 ~ 4s内,回路中的感应电动势
E=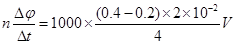 =1V;
=1V;
(2)t = 5s时,磁场强度正在减弱,故线圈产生的感应电流的磁场要阻碍这种减弱,所以感应电流产生的磁场方向是垂直纸面向里的,故a点的电势高于b点;
(3)在t = 5s时,线圈的感应电动势为E1= =4V;
=4V;
电路中的电流为I1=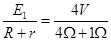 =0.8A;
=0.8A;
故电阻两端的电压U=I1×R=0.8A×4Ω=3.2V。
考点:法拉第电磁感应定律,欧姆定律。
本题难度:一般
4、选择题 下列现象中,能表明电和磁有联系的是 ( )
A.摩擦起电
B.两块磁铁相互吸引或排斥
C.带电体静止不动
D.磁铁插入闭合线圈过程中,线圈中产生感应电流