1、计算题 下图是某种静电分选器的原理示意图。两个竖直放置的平行金属板带有等量异号电荷,形成匀强电场。分选器漏斗的出口与两板上端处于同一高度,到两板距离相等。混合在一起的a、b两种颗粒从漏斗出口下落时,a种颗粒带上正电,b种颗粒带上负电。经分选电场后,a、b两种颗粒分别落到水平传送带A、B上。已知两板间距d=0.1m,板的度l=0.5m,电场仅局限在平行板之间;各颗粒所带电量大小与其质量之比均为1×10-5 C/kg。设颗粒进入电场时的初速度为零,分选过程中颗粒大小及颗粒间的相互作用力不计。要求两种颗粒离开电场区域时,不接触到极板但有最大偏转量。重力加速度g取10m/s2。
(1)左右两板各带何种电荷?两极板间的电压多大?
(2)若两带电平行板的下端距传送带A、B的高度H=0.3m,颗粒落至传送带时的速度大小是多少?
(3)设颗粒每次与传带碰撞反弹时,沿竖直方向的速度大小为碰撞前竖直方向速度大小的一半。写出颗粒第n次碰撞反弹高度的表达式。并求出经过多少次碰撞,颗粒反弹的高度小于0.01。

参考答案:解:(1)左板带负电荷,右板带正电荷
依题意,颗粒在平行板间的竖直方向上满足l=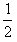 gt2
gt2
在水平方向上满足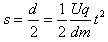
两式联立得
(2)根据动能定理,颗粒落到水平传送带上满足
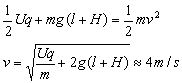 ?
?
(3)在竖直方向颗粒作自由落体运动,它第一次落到水平传送带上沿竖直方向的速度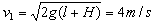
反弹高度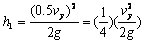
根据题设条件,颗粒第n次反弹后上升的高度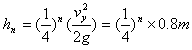
当n=4时,hn<0.01m
本题解析:
本题难度:困难
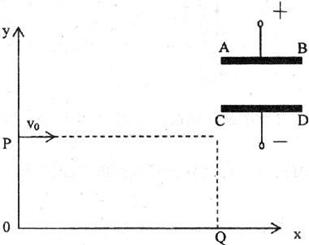
2、计算题 如图,P点的坐标为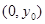 ,Q点的坐标为
,Q点的坐标为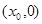 ,平行板电容器AB、CD两带电板平行于x轴,上板带正电,板长为
,平行板电容器AB、CD两带电板平行于x轴,上板带正电,板长为 ,两板间的距离为
,两板间的距离为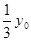 ,现有一质量为m,电量为+q的带电粒子从P点以初速度大小
,现有一质量为m,电量为+q的带电粒子从P点以初速度大小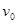 垂直于y轴射入第一象限,欲使这个粒子从Q点射出,且有最大的偏转角,需将电容器平移至第一象限的适当位置,不计粒子的重力,求
垂直于y轴射入第一象限,欲使这个粒子从Q点射出,且有最大的偏转角,需将电容器平移至第一象限的适当位置,不计粒子的重力,求
(1)粒子从P点运动到Q点的时间;
(2)电容器平移至第一象限后上板左端A点的坐标位置(忽略板的厚度)
(3)电容器两板的电压U值为多少?
参考答案:(1)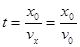 (2)
(2)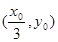 (3)
(3)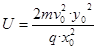
本题解析:
(1)带电粒子整个运动过程中,其沿x轴的分速度vx始终不变,即vx=v0,所以从P点运动到Q点的时间: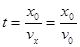
(2)设板长为2a,两板间的距离为d即a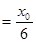 ,d=
,d=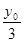 ,粒子平行x轴射入电场,经电场偏转射出,设两板的电势差为U,射出电场时沿y轴方向的位移为y,沿y轴方向的速度分量为vy,则有:
,粒子平行x轴射入电场,经电场偏转射出,设两板的电势差为U,射出电场时沿y轴方向的位移为y,沿y轴方向的速度分量为vy,则有:
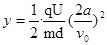 (1)
(1)
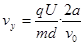 (2)
(2)
所以: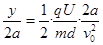 (3)
(3)
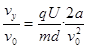 (4)
(4)
所以: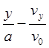 (5)
(5)
由(5)式可知,射出电场后粒子的速度反向延长线会经过它在电场中的水平位移的中点M。
欲使这个粒子有最大的偏转角,粒子在电场中的偏转位移就应该最大,
即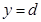 (6)
(6)
粒子必须从紧靠上板的位置射入电场,从Q点射出,应该有M、D、Q三点共线,如图所示。
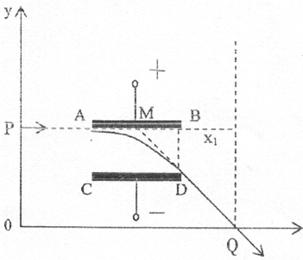
设B点离过Q点的竖直线距离为x1,
则有: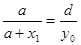 (7)
(7)
解得: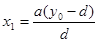 (8)
(8)
所以,A点的横坐标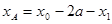 (9)
(9)
即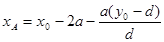 (10)
(10)
将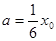 ,
,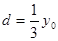 代入(10)式得:
代入(10)式得:
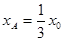 (11)
(11)
即A点的坐标位置为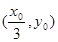
(3)由(1)、(6)得:
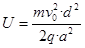 (12)
(12)
将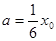 ,
,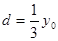 代入(12)式得:
代入(12)式得:
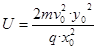 (13)
(13)
本题难度:困难
3、计算题 如图所示,ab、cd为一对水平正对放置的平行金属板,ab板在上、cd板在下,两板间距d=0.10m,板长l=2.0m,两板间电势差U=1.0×104V。一带负电荷的油滴以初速度v0=10m/s由两板中央沿垂直电场强度方向射入板间电场区,并能由bd端射出电场区。设电场区域仅限于两平行板之间,取g=10m/s2
小题1:说明在带电油滴的比荷大小(q/m)不同时,油滴射入电场后可能发生的几种典型运动情况,指出运动性质。
小题2:求出上述几种典型运动情况中油滴的比荷大小(q/m)应满足的条件。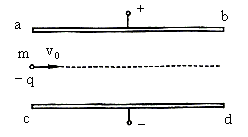
参考答案:
小题1:见解析
小题2:见解析
本题解析:
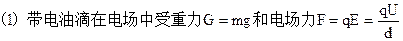
因为G和F均为恒力,所以有以下三种典型的运动情况:
 ?
?

 ?
?
(2)①在电场力大于重力的情况下,当油滴沿竖直方向的位移满足
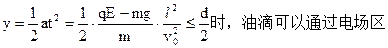 ?
?
因此在电场力大于重力的情况下油滴的比荷应满足
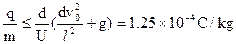 ?
?
②在电场力等于重力的情况下,应有qU/d=mg?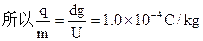 ?
?
③在电场力小于重力的情况下,当油滴沿竖直方向的位移满足

因此在电场力小于重力的情况下油滴的比荷应满足
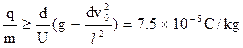 ?
?
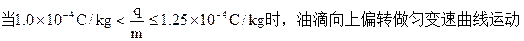
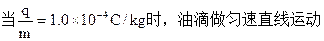
本题难度:一般
4、计算题 如图所示,一质量为m、电量为+q、重力不计的带电粒子,从A板的S点由静止开始释放,经A、B加速电场加速后,穿过中间偏转电场,再进入右侧匀强磁场区域.已知AB间的电压为U,MN极板间的电压为2U,MN两板间的距离和板长均为L,磁场垂直纸面向里、磁感应强度为B、有理想边界.求:

(1)带电粒子离开B板时速度v0的大小;
(2)带电粒子离开偏转电场时速度v的大小与方向;
(3)要使带电粒子最终垂直磁场右边界射出磁场,磁场的宽度d多大?
参考答案:(1)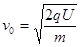 (2)
(2) 方向与水平方向成450角(3)
方向与水平方向成450角(3)
本题解析:(1)带电粒子在加速电场中,由动能定理得: 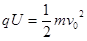
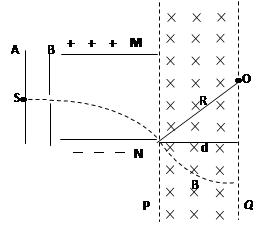
得带电粒子离开B板的速度: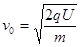
(2)粒子进入偏转电场后,有: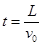 ,
,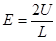 ?,
?,
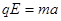 ?,?
?,?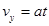 ?解得 :
?解得 :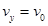
则粒子离开偏转电场时的速度大小:
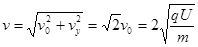 ,方向与水平方向成450角.
,方向与水平方向成450角.
(3)粒子进入磁场后,据牛顿第二定律得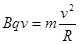 由几何关系得
由几何关系得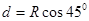 解得
解得 .
.
点评:本题考查了带电粒子在场中的运动,包括类平抛和圆周运动,考查类型非常有代表性。
本题难度:一般
5、简答题 如图19所示,一带电量为 、质量为
、质量为 的小球,从距地面高
的小球,从距地面高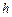 处以一定的初速度水平抛出,在距抛出点水平距离为
处以一定的初速度水平抛出,在距抛出点水平距离为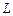 处有根管口比小球略大的竖直细管,管的上口距地面的
处有根管口比小球略大的竖直细管,管的上口距地面的 。为了使小球能无碰撞地通过管子,可在管子上方整个区域内加一水平向左的匀强电场,求:
。为了使小球能无碰撞地通过管子,可在管子上方整个区域内加一水平向左的匀强电场,求:
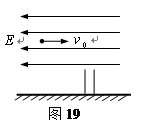
(1)小球的初速度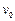 的大小;
的大小;
(2)应加电场的场强大小;
(3)小球落地时的动能。
参考答案:⑴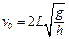 ?⑵
?⑵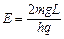 ?⑶
?⑶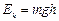
本题解析:本题涉及到自由落体运动、匀减速直线运动等多过程及多种规律。如运动学公式、牛顿第二定律、动能定理等的运用,考查学生对复杂过程的综合分析能力和物理规律的综合运用能力。
要使小球无碰撞地通过管口,则当它到达管口时,速度方向为竖直向下,
(1)?竖直方向小球做自由落体运动,则运动时间为: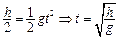
水平方向小球做匀减速运动,减速至0,位移为: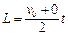 ?
?
解得?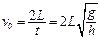 ?
?
(2)水平方向,根据牛顿第二定律 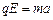
又由运动学公式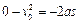
解得:?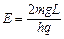 ?
?
(3)由动能定理得 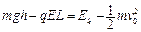 ?
?
解得?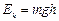
本题难度:一般