1、简答题  一台二氧化碳激光器发出的激光功率为P="1" 000 W，出射光束截面积为A="1" mm2,这束光垂直射到温度为T="273" K，厚度为d="2" cm的铁板上，如果有80%的光束能量被激光照射到那一小部分铁板所吸收，并使其熔化成与光束等截面积的直圆柱孔，需要多少时间？铁的有关参数：热容量c="26.6" J/mol·K，密度ρ=7.90×103 kg/m3,熔点Tm="1" 798 K,熔解热L=1.49×104 J/mol,摩尔质量U=56×10-3 kg。

参考答案：0.192 s

本题解析：激光所照射到的质量为M的部分铁板在熔化过程中所吸收的热量为Q=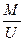(cΔT+L)="Pt·80%?" 其中质量M=Adρ。代入数据求得t="0.192" s

本题难度：简单

2、计算题  如图所示，巡查员站立于一空的贮液池边，检查池角出液口的安全情况．已知池宽为L，照明灯到池底的距离为H，若保持照明光束方向不变，向贮液池中注入某种液体，当液面高为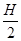时，池底的光斑距离出液口.

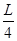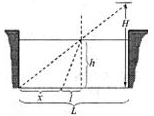
(1)试求当液面高为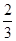H时，池底的光斑到出液口的距离x.
(2)控制出液口缓慢地排出液体，使液面以vh的速率匀速下降，试求池底的光斑移动的速率vx.

参考答案：(1) x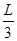＝(2) vx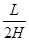＝·vh.

本题解析：(1)作出光路图如图所示．? --------（1分）
由几何关系知：
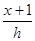＝?①? ---------（2分）
由折射定律：
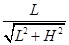＝n·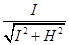?②? ---------（2分）
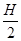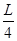代入h＝、l＝得：
n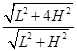＝?③? --------（1分）
联立①②③式得x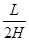＝·h.?--------（2分）
当h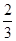＝H时，解得x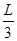＝.? --------（1分）
(2)由x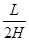＝·h知，Δx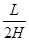＝·Δh，? ---------（1分）
则?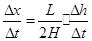，?---------（1分）
即vx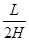＝·vh.?---------（2分）
本题考查光的折射现象，先根据题目所给条件画出光路图，由光路图结合几何关系求解

本题难度：一般

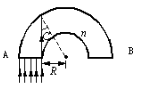
3、计算题  主截面是边长为d的正方形的棱柱，折射率为n，将其弯成半圆形（如图20－26所示）．要使A端垂直入射的光线全部从B端射出，求所弯半圆形的最小内半径R的值．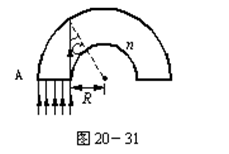

参考答案：R＝d/（n－1）。

本题解析：要使光线全部由B端射出，则要求射入棱柱的光线全部发生全反射，而不能发生折射。那么从A端入射的光线中，只要使最易发生折射的光线发生全反射，则可满足题目要求。最易发生折射的光线应为入射角最小的光线，由图可看出A端最内侧的光线其入射角最小，因此必须保证此光线能发生全反射，即此光线的入射角等于或大于临界角．由图中的几何关系可看出，此光线入射角的正弦值为：sinC＝R/（R＋d）（由折射定律可知sinC=），由此可解得半圆的最小内半径为R＝d/（n－1）。

本题难度：简单

4、实验题  一台激光器，它的功率为P，如果它射出的单色光在空气中的波长为λ，则这束单色光的频率是_________________，它在时间t内辐射的光能为_________________，如果已知这束单色光在某介质中的传播速度为v，那么这束单色光从该介质射向真空发生全反射的临界角为_________________.

参考答案：c/λ? Pt? arcsin（v/c）

本题解析：根据v=λf可得这束单色光的频率为f=c/λ；
激光器在时间t内做的功W=Pt转化为光能；
这束单色光对该介质的折射率n=c/v，设它从该介质射向真空发生全反射的临界角为C，则sinC=1/n=v/c，所以C=arcsin=.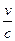

本题难度：简单

5、计算题  为从军事工事内部观察外面的目标，在工事壁上开一长方形孔，设工事壁厚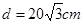，孔的宽度L=20cm,孔内嵌入折射率为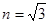的玻璃砖如图所示，试求：

(1)嵌入玻璃砖后，工事内部人员观察到外界的视野的最大张角为多少？
(2)要想使外界180°范围内景物全被观察到，则应嵌入多大折射率的玻璃砖？

参考答案：(1) 120°(2) n＝2

本题解析：工事内的人从内壁左侧能最大范围观察右边的目标，如图所示。

已知d＝34.64 cm，L＝20 cm，tanβ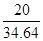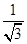＝≈，所以β＝30°。
(1)由折射定律有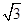＝，得α＝60°。即视野的张角最大为120°。
(2)要使视野的张角为180°，即α′＝90°，由折射定律有＝n，所以n＝2

本题难度：简单