1、选择题  如图所示，质量相同的三个小球从足够长的斜面上同一点O分别以初速度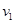、、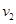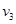水平抛出，落在斜面上的位置分别是A、B、C，已知OA=AB=BC，空气阻力不计，则?（?）
A．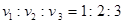
B．飞行过程中动能增量之比为1：：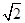
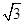
C．飞行时间之比为1：：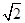
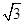
D．落在斜面时的动能之比为1：2：3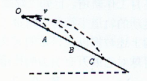

参考答案：CD

本题解析：小球均做平抛运动，落到斜面上，所以，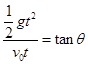
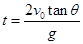
又因为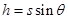，OA=AB=BC，所以飞行时间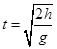之比为1：：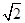
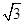
所以初速度之比为：1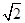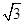：：C对；A错；动能增加等于重力做功，因为高度之比为1：2：3，所以动能增量为1：2：3，B错；落到斜面的动能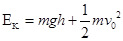，因为初速度之比为：1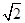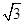：：，所以初动能之比为1：2：3，高度之比为1：2：3，重力做功之比为1：2：3，所以落到斜面的动能之比为1：2：3，故D正确，故答案选CD.

本题难度：简单

2、简答题  如图所示，一个长L1=0.9m、宽L2=0.6m的光滑斜面体，其倾角θ=30°．有一长度L=0.4m的轻质绳一端固定在距斜面顶点A为L=0.4m斜面边缘的O点上，另一端系一质量m=1kg的小球．现把小球拉至顶点A处，以v0=1m/s的初速度沿斜面顶边缘水平抛出．（g取10m/s2）
（1）刚开始小球做什么运动？并说明理由．
（2）求小球运动至斜面边缘B点时受到绳子的拉力FT．
（3）若小球运动至B点时绳子刚好断了，求小球从斜面上飞出后落地点与最初抛出点在地面上投影点的距离L3．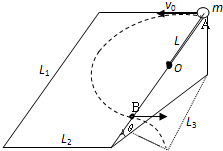

参考答案：

（1）小球沿斜面向下的加速度a=mgsinθm=5m/s2
其在斜面上运动可等效看作在g′=a=5m/s2的竖直平面上的曲线运动
由于小球刚抛出的速度v0＜

本题解析：

本题难度：一般

3、简答题  2010年冬奥会在加拿大温哥华举行，跳台滑雪是冬奥会中最壮观而刺激的项目．运动员从100多米长的助滑道俯冲而下，37度的陡坡到末段急剧减小为11度左右的缓坡，运动员在起跳点以每小时100公里左右的速度腾空而起，展开又宽又长的滑雪板“飞行”约6秒钟，落在着陆道的K点．巍巍跳台虽然高达几十米，但运动员身体和地面相对高度却始终不过数米，斜坡的弧度和运动员在空中的抛物线轨迹大致平行．当运动员最后以极小的角度落地时，垂直于地面的冲击力远远小于三级跳远之类的田径项目，何况还有40厘米厚的雪层缓冲，难怪总会是“有惊无险”的．假设助滑道长度l=108m，坡度θ=37°，末端水平且水平长度忽略不计，运动员在空中飞行的时间t=6s．已知重力加速度g取10m/s2，sin37°=0.6，cos37°=0.8，不计运动员所受阻力．
（1）运动员起跳速度是多大？
（2）运动员着陆位置与出发位置的高度差和水平距离分别是多大？

参考答案：（1）设运动员起跳的速度为υ，由动能定理有mglsinθ=12mv2
代入数据，解得v=

本题解析：

本题难度：一般

4、选择题  在同一水平直线上的两位置分别沿同方向水平抛出两小球A和B，其运动轨迹如图所示，不计空气阻力，要使两球在空中相遇，则必须（　　）
A．先抛出A球
B．先抛出B球
C．同时抛出两球
D．A球的初速度大于B球的初速度