1、计算题  一个质量为M的雪橇静止在水平雪地上，一条质量为m的爱斯基摩狗站在该雪橇上。狗向雪橇的正后方跳下，随后又追赶并向前跳上雪橇；其后狗又反复地跳下、追赶并跳上雪橇，狗与雪橇始终沿一条直线运动。若狗跳离雪橇时雪橇的速度为V，则此时狗相对于地面的速度为V+u(其中u为狗相对于雪橇的速度，V+u为代数和。若以雪橇运动的方向为正方向，则V为正值，u为负值)。设狗总以速度v追赶和跳上雪橇，雪橇与雪地间的摩擦忽略不计。已知v的大小为5m/s，u的大小为4m/s，M=30kg，m=10kg。
（1）求狗第一次跳上雪橇后两者的共同速度的大小。
（2）求雪橇最终速度的大小和狗最多能跳上雪橇的次数。（供使用但不一定用到的对数值：lg2=0.301，lg3=0.477)

2、计算题  （16分）如图所示，在倾角θ＝30?的斜面上放置一段凹槽B，B与斜面间的动摩擦因数μ＝，槽内靠近右侧壁处有一小球A，它到凹槽内左壁侧的距离d＝0.10m．A、B的质量都为m=2.0kg，B与斜面间的最大静摩擦力可认为等于滑动摩擦力，不计A、B之间的摩擦，斜面足够长．现同时由静止释放A、B，经过一段时间，A与B的侧壁发生碰撞，碰撞过程不损失机械能，碰撞时间极短．取重力加速度g=10m/s2．求：

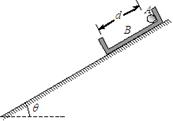
（1）A与B的左侧壁第一次发生碰撞后瞬间A、B的速度．
（2）在A与B的左侧壁发生第一次碰撞后到第二次碰撞前的这段时间内，A与B的左侧壁的距离最大可达到多少？

3、选择题  三木块从同一高度同时开始自由下落，其中木块甲自由落体；木块乙在刚刚开始下落时被一颗子弹沿水平方向击中并留在其中；木块丙在下落途中被一颗子弹沿水平方向击中并留在其中。不计空气阻力及子弹进入木块的时间，则（?）
A．三块木块同时落地
B．甲木块最先落地，乙、丙同时落地
C．木块丙最后落地，甲、乙同时落地
D．甲、乙、丙依次先后落地

4、选择题  质量为M的小车，以速度v在光滑水平面上前进，车上站着质量为m的人，当人以相对车的速度u向车后水平跳出，车速变为v0.若取v0方向为正，则
A.（m+M）v0=Mv
B.（m+M）v0=Mv-mu
C.（m+M）v0=Mv+m(u+v)
D.（m+M）v0=Mv-m(u-v)

5、选择题  2005年7月26日，美国“发现号”航天飞机从肯尼迪航天中心发射升空，飞行中一只飞鸟撞上了航天飞机的外挂油箱，幸好当时速度不大，航天飞机有惊无险．假设某航天器的总质量为10吨，以2km/s的速度高速运行时迎面撞上一只速度为10m/s、质量为5kg的大鸟，碰撞时间为1．0×10-5s，则撞击过程中的平均作用力约为(? )
A．2×109N
B．1×109N
C．1×1012N
D．2×106N