1、选择题  如图所示，将一个光滑、绝缘的挡板ABCD固定在光滑、绝缘的水平面上，AB段为直线形挡板， BCD段是半径为R的圆弧形挡板，且AB与BCD相切。挡板处于场强为E的匀强电场中，电场方向与圆直径MN平行。现将带电量为q、质量为m的小球从挡板内侧的A点由静止释放，小球沿挡板内侧恰好过M点运动到D点后抛出，下列判断正确的是?

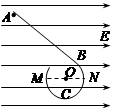
A．小球带正电或带负电均可完成上述运动过程
B．小球运动到N点时动能最大
C．AN两点间沿电场线方向的距离为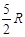
D．小球运动到C点时，挡板对小球的弹力为3qE

参考答案：BCD

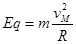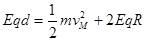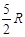本题解析：根据小球的受力情况可知，小球只能带正电才可完成上述运动过程；小球运动到N点时，电场力做功最多，所以动能最大；因为小球沿挡板内侧恰好过M点，则,，解得d=;小球运动到C点时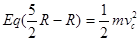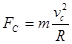，?，解得Fc=3qE.。选项BCD正确。

本题难度：一般

2、简答题  一质量为m=40kg的小孩子站在电梯内的体重计上．电梯从t=0时刻由静止开始上升，在0s到6s内体重计示数F的变化如图所示．试问：在这段时间内电梯上升的高度是多少？（取重力加速度g=10m/s2．）

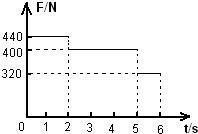
参考答案：在0s-2s内，电梯做匀加速运动，加速度为：a1=F1-mgm=1m/s2
上升高度为h1=12a1t12=2m
2s末速度为v=a1t1=2m/s
在中间3s内，电梯加速度为0，做匀速运动
上升高度h2=vt2=6m
最后1s内做匀减速运动，加速度a2=F3-mgm=-2m/s2在第6s末恰好停止．
上升高度为h3=12vt3=1m
故在这段时间内上升高度为h=h1+h2+h3=2+6+1m=9m
答：在这段时间内电梯上升的高度是为9m．

本题解析：

本题难度：一般

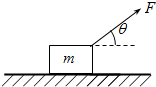
3、计算题  如图所示，用与水平方向成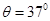的恒力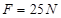拉一个质量为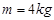的物体，由静止开始在水平地面沿直线运动，经过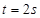物体位移为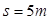，取重力加速度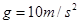。试求：

（1）拉力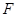对物体所做的功；
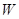（2）物体获得的动能；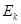
（3）物体与地面间的动摩擦因数。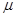

参考答案：（1）100J（2）50J（3）0.4

本题解析：（1）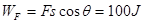
（2）由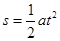得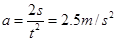
?
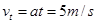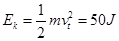
由动能定理得：?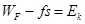
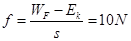
根据牛顿第二定律：?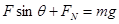

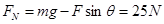
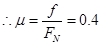
点评：本题难度较小，应首先分析受力情况和运动情况，确定研究对象和研究过程

本题难度：一般

4、简答题  为了使航天员能适应在失重环境下的工作和生活，国家航天局组织对航天员进行失重训练．故需要创造一种失重环境；航天员乘坐到民航客机上后，训练客机总重5×104kg，以200m/s速度沿30°倾角爬升到7000米高空后飞机向上拉起，沿竖直方向以200m/s?的初速度向上作匀减速直线运动，匀减速的加速度为g，当飞机到最高点后立即掉头向下，仍沿竖直方向以加速度为g加速运动，在前段时间内创造出完全失重，当飞机离地2000米高时为了安全必须拉起，后又可一次次重复为航天员失重训练．若飞机飞行时所受的空气阻力f=Kv（k=900N?s/m），每次飞机速度达到350m/s?后必须终止失重训练（否则飞机可能失速）．
求：（1）飞机一次上下运动为航天员创造的完全失重的时间．
（2）飞机下降离地4500米时飞机发动机的推力（整个运动空间重力加速度不变）．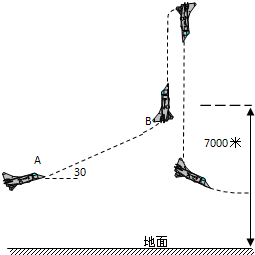

参考答案：（1）上升时间t上=v0g=20s?上升高度h上=v202g=2000m
判断当速度达到350m/s时，下落高度h下=v212g=6125m，
此时离地高度为h+h上-h下=7000+2000-6125=2875＞2000m，t下=v1g=35s，
所以一次上下创造的完全失重的时间为55s．
（2）当飞机在离地4500m＞2875m，所以飞机仍在完全失重状态，飞机自由下落的高度h2=2000+7000-4500m，此时，v2=

本题解析：

本题难度：一般

5、选择题  质量为2m的物体A与水平面间的摩擦可以忽略不计，质量为m的物体B与地面的动摩擦因数为μ．A、B并排放置在水平面上，用在水平推力F的作用下，共同向右做加速运动．此时（　　）
A．A对B的推力可能小于μmg
B．若μ=0则A对B的推力等于零
C．B对A的推力可能小于

参考答案：设A对B的推力为N．
A、由题意，B向右加速运动，具有向右的加速度，B所受的滑动摩擦力大小为μmg，方向向左，则根据牛顿第二定律得知合外力向右，所以A对B的推力一定大于μmg．故A错误．
B、若μ=0，根据牛顿第二定律得：
对整体：a=F3m，
对B：A对B的推力N=ma=F3≠0．故B错误．
C、D对整体，则有：F-μmg=3ma，得F=μmg+3ma
对B；N-μmg=ma，得N=μmg+ma
若μ=0，联立解得，N=F3；若μ≠0，解得，N＞F3．故C错误，D正确．
故选D

本题解析：

本题难度：简单