1、选择题 如图所示,在光滑的桌面上有M、m两个物块,现用力F推物块m,使M、m两物块在桌上一起向右加速,则M、m间的相互作用力为

[? ]
A.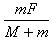
B.
C.若桌面的摩擦因数为μ,M、m仍向右加速,则M、m间的相互作用力为
D.若桌面的摩擦因数为μ,M、m仍向右加速,则M、m间的相互作用力仍为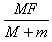
参考答案:BD
本题解析:
本题难度:一般
2、选择题 如图所示,水平木板上有质量m=1.0kg的物块,受到随时间t变化的水平拉力F作用,用力传感器测出相应时刻物块所受摩擦力Ff的大小.取重力加速度g=10m/s2,下列判断正确的是( )
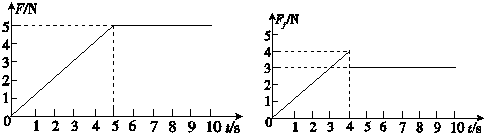
A.4s内拉力对物块做功为零
B.4s末物块所受合力大小为4.0N
C.物块与木板之间的动摩擦因数为0.3
D.6s~9s内物块的加速度大小为2.0m/s2
参考答案:A、在0-4s内,物体所受的摩擦力为静摩擦力,4s末开始运动,故4s内拉力做功为零,故A正确;
B、4s末拉力为4N,摩擦力为4N,合力为零.故B错误.
C、由图可知,滑动摩擦力为3N,则由f=μmg;解得μ=fmg=310=0.3;故C正确;
D、由图可知拉力为5N,摩擦力为3N,则合力F合=F-f=5-3=2N;故加速度为:a=F合m=2.0m/s2;故D正确;
故选:ACD.
本题解析:
本题难度:一般
3、简答题 质量为8×107kg的列车,从某处开始进站并关闭动力,只在恒定阻力作用下减速滑行。已知它开始滑行时的初速度为20m/s,当它滑行了300米时,速度减小到10m/s,接着又滑行了一段距离后停止,那么:
(1) 关闭动力时列车的初动能为多大?
(2) 列车受到的恒定阻力为多大?
(3)列车进站滑行的总距离和总时间各为多大?
参考答案:(1)1.6×1010J
(2) 4×107N
(3)400 m
本题解析:(1)初动能Ek0=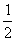 mv20 =
mv20 =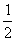 ×8×107×202=1.6×1010J
×8×107×202=1.6×1010J
(2) 恒定阻力大小:f = m|a|=m(v20-v21)/2s=4×107N
(3)设总时间和总位移大小分别为t0和s0,则:
ft0=mv0
f s0= mv20
mv20
则:t0=mv0/f="40" s
s0= mv20/f="400" m
mv20/f="400" m
本题难度:一般
4、简答题 如图所示是建筑工地上常用的一种“深穴打夯机”,电动机带动两个滚轮匀速转动将夯杆从深坑提上来,当夯杆底端刚到达坑口时,两个滚轮彼此分开,将夯杆释放,夯杆在自身重力作用下,落回深坑,夯实坑底,夯杆不反弹,设夯杆与坑底的接触时间为t=1.0s,然后两个滚轮再次压紧,将夯杆提上来,如此周而复始.已知两个滚轮边缘的线速度恒为v=4.0m/s,每个滚轮对夯杆的正压力均为F=2.0×104N,滚轮与夯杆间的动摩擦因数μ=0.30,夯杆质量m=1.0×103kg,坑深h=6.4m.假定在打夯的过程中坑的深度不变,g=10m/s2,求:
(1)从夯杆开始向上运动到刚开始匀速运动,夯杆上升的高度H是多少?
(2)每个打夯周期(从夯杆刚离开坑底到下一次夯杆刚离开坑底的时间)中,电动机对夯杆做的功W;
(3)打夯周期T.

参考答案:(1)对夯杆由牛顿第二定律得:
2μF-mg=ma,解得:a=2m/s2,
当夯杆速度增加到4m/s时,
夯杆上升的高度为:H=v22a,
解得:H=4m;
(2)电动机对夯杆所做的功等于夯杆增加的机械能,
W=EP+EK=mgh+12mv2=1.0×103×10×6.4+12×1.0×103×42=7.2×104J;
(3)夯杆从开始运动到落回原处共经历四个运动过程:
向上匀加速运动、向上匀速运动、向上竖直上抛运动,向下自由落体运动.
匀加速运动的时间t1=va=4m/s2m/s2=2s,
匀速运动的时间t2=h-Hv=6.4m-4m4m/s=0.6s,
竖直上抛上升过程的运动时间t3=vg=4m/s10m/s2=0.4s,
竖直上抛的位移h′=v22g=422×10=0.8m,
自由落体运动:h+h′=12gt42,
t4=
本题解析:
本题难度:一般
5、简答题 如图所示,在两条平行的虚线内存在着宽度为L、场强为E的匀强电场,在与右侧虚线相距也为L处有一与电场平行的屏.现有一电荷量为+q、质量为m的带电粒子(重力不计),以垂直于电场线方向的初速度v0射入电场中,v0方向的延长线与屏的交点为O.试求:
(1)粒子在电场中运动的时间;
(2)粒子刚射出电场时的速度方向与初速度方向间夹角的正切值tanα;
(3)粒子打到屏上的点P到O点的距离Y.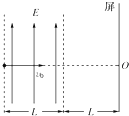
参考答案:(1)粒子在垂直于电场线的方向上做匀速直线运动,则粒子在电场中运动的时间的时间t=Lv0.
(2)设粒子射出电场时沿平行电场线方向的速度为vy,根据牛顿第二定律,粒子在电场中的加速度为:a=qEm
所以vy=at=aLv0=qELmv0
所以粒子刚射出电场时的速度方向与初速度方向间夹角的正切值为tanα=vyv0=qELmv20.
(3)设粒子在电场中的偏转距离为y,则y=12at2=12?qELmv0t2
又Y=y+Ltanα?
解得:Y=3qEL22mv20
答:
(1)粒子在电场中运动的时间是Lv0;
(2)粒子刚射出电场时的速度方向与初速度方向间夹角的正切值tanα为qELmv20;
(3)粒子打到屏上的点P到O点的距离Y是3qEL22mv20.
本题解析:
本题难度:一般