1、简答题  如图所示，一个半径R=1.0m的圆弧形光滑轨道固定在竖直平面内，轨道的一个端点C和圆心O的连线与竖直方向夹角θ=45°，A为轨道最低点，B为轨道最高点．一个质量m=0.50kg的小球从空中D点以V0=6m/s的速度水平抛出，恰好从轨道的C端沿切线方向进入轨道，重力加速度g=10m/s2，求：
（1）小球抛出点D距圆轨道C端的水平距离L．
（2）小球经过轨道最低点A时，受到轨道的作用力FA．
（3）判断小球能否到达最高点B，说明理由．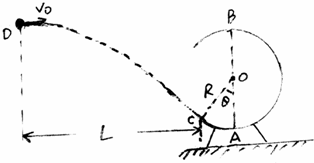

参考答案：（1）小球抛出后做平抛运动，小球恰好从轨道的C端沿切线方向进入轨道，说明小球的末速度应该沿着C点切线方向，
将平抛末速度进行分解，根据几何关系得：
C点速度在竖直方向的分量：vy=v0tan45°=6m/s
竖直方向的分运动为自由落体运动，t=vyg=0.6s
水平方向做平抛运动，L=v0t=3.6m
（2）由机械能守恒定律，有
12mvC2+mg(R-Rcos45°)=12mvA2
根据向心力公式得：
FA-mg=mvA2R
解得：FA=43.9N
（3）设小球能到达B点，根据机械能守恒定律，有
12mv02+mg(h-R-Rcos45°)=12mvB2
解得：vB=

本题解析：

本题难度：一般

2、选择题  关于物体的运动，下列说法中正确的是（　　）
A．匀速圆周运动的物体所受合外力是恒力
B．斜抛运动的加速度大小恒定，方向时刻变化
C．做匀变速运动的物体，其轨迹一定是直线
D．物体的速度与加速度的方向不在同一条直线时，物体一定做曲线运动

参考答案：A、匀速圆周运动物体所受合力提供向心力，方向始终指向圆心，合外力不是恒力．故A错误．
B、斜抛运动仅受重力，加速度的大小和方向都不变．故B错误．
C、匀变速直线运动的物体，轨迹不一定是直线，可能是曲线．故C错误．
D、物体的速度与加速度的方向不在同一条直线时，物体一定做曲线运动．故D正确．
故选D．

本题解析：

本题难度：简单

3、选择题  关于匀速圆周运动的向心力，下列说法错误的是（　　）
A．向心力是指向圆心方向的合力，是根据力的作用效果命名的
B．向心力可以是多个力的合力，也可以是其中一个力或一个力的分力
C．对稳定的圆周运动，向心力是一个恒力
D．向心力的效果是改变质点的线速度的方向

参考答案：A、向心力是物体做匀速圆周运动所需要的指向圆心的合外力，故它是根据力的作用效果命名的．所以A正确；
B、向心力是物体做匀速圆周运动所需要的指向圆心的合外力，所以它可以由一个力提供，也可以由几个力的合力提供，也可以一个力的分力提供，故B正确；
C、向心力是指向圆心的合外力，所以它不是一个恒力．故C不正确；
D、由于向心力指向圆心，与线速度方向始终垂直，所以它的效果只是改变线速度方向，不会改变线速度大小．故D不正确；
本题选错误的，故选C

本题解析：

本题难度：一般

4、选择题  如图所示，质量为m的滑块从h高处的a点沿圆弧轨道ab滑入水平轨道bc，滑块与轨道的动摩擦因素相同．滑块在a、c两点时的速度大小均为v，ab弧长与bc长度相等．空气阻力不计，则滑块从a?到c?的运动过程中（　　）
A．小球的动能始终保持不变
B．小球在bc过程克服阻力做的功一定等于mgh/2
C．小球经b点时的速度小于

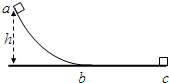
参考答案：A、块在a、c两点时的速度大小均为v，知滑块先加速和减速．动能先增加后减小．故A错误．
B、对全程运用动能定理得，mgh-Wf=0，全程克服阻力做功等于mgh，因为ab段所受的支持力不等于重力，所以所受的摩擦力与bc段不等，克服摩擦力做功不等，则小球在bc过程克服阻力做的功不等于mgh2．故B错误．
C、D、根据动能定理得：mgh-Wf′=12mv′2-12mv2，因为Wf′＞mgh2，所以v′＜

本题解析：

本题难度：一般

5、简答题  如图所示，用长为l的绝缘细线拴一个质量为m、带电量为+q的小球（可视为质点）后悬挂于O点，整个装置处于水平向右的匀强电场E中．将小球拉至使悬线呈水平的位置A后，由静止开始将小球释放，小球从A点开始向下摆动，当悬线转过60°角到达位置B时，速度恰好为零．求：
（1）B、A两点的电势差UBA
（2）电场强度E
（3）小球到达B点时，悬线对小球的拉力T．

参考答案：（1）小球由A到B过程中，由动能定理得：
? mgLsin60°+qUAB=0
所以UAB=-

本题解析：

本题难度：一般