1、简答题  如图所示，光滑水平地面上停着一辆平板车，其质量为2m，长为L，车右端（A点）有一块静止的质量为m的小金属块．金属块与车间有摩擦，以中点C为界，AC段与CB段摩擦因数不同．现给车施加一个向右的水平恒力，使车向右运动，同时金属块在车上开始滑动，当金属块滑到中点C时，撤去这个力．已知撤去力的瞬间，金属块的速度为v0，车的速度为2v0，最后金属块恰好停在车的左端（B点）．如果金属块与车的AC段间的动摩擦因数为μ1，与CB段间的动摩擦因数为μ2，求μ1与μ2的比值．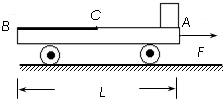

参考答案：金属块由A→C过程中做匀加速运动，加速度为：
a1=fm=μ1mgm=μ1g?
设金属块由A到达C历时为t1，速度v0=a1t1…①
小车加速度a2=2a1=2μ1g．?
车此刻的速度：2v0=a2t1…②
金属块与小车位移之差：s=12a2t12-12a1t12=12(2μ1g-μ1g)(v0μ1g)2，
而s=L2，
所以：μ1=v02gL…③
从小金属块滑至车中点C开始到小金属块停在车的左端，它与车有共同速度，设为v，此过程中，系统水平方向动量守恒，有　
2m×2v0+mv0=（2m+m）v，
得v=53v0．?
此过程中系统动能损失为μ2mgL2=12mv02+12×2m×(2v0)2-12×3m×(53v0)2，
解得：μ2=2v023gL…④
③④?得：μ1μ2=32．?
答：μ1与μ2的比值为3：2．

本题解析：

本题难度：一般

2、简答题  如图所示，粗糙斜面其倾角为α，底端通过长度可忽略的光滑小圆弧与光滑水平面连接．．A、B是两个质量均为?m=1㎏的小滑块（可视为质点），B的左端连有轻质弹簧，处于静止状态．当滑块A置于斜面上且受到大小F=4N，方向垂直斜面向下的恒力作用时，恰能沿斜面向下匀速运动．现撤去F，让滑块A从斜面上距斜面底端L=1m处由静止开始下滑，若取g=10m/s2，sinα=0.6，cosα=0.8．求：
（1）滑块A与斜面的动摩擦因数μ；
（2）滑块A到达斜面底端时的速度大小v1；
（3）滑块A在斜面上运动的加速度大小a；
（4）滑块A开始与弹簧接触到此后两滑块和弹簧构成的系统在相互作用过程中，弹簧的最大弹性势能Ep．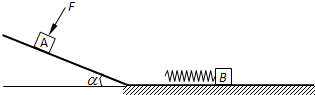

参考答案：（1）滑块A匀速下滑时，受重力mg、恒力F、斜面支持力FN和摩擦力Fμ作用，
由平衡条件有mgsinα=μFN①
FN=mgcosα+F②
即联立①②并化简后得μ=mgsinαmgcosα+F③
代入数据解得动摩擦因数μ=0.5
（2）撤去F后，滑块A匀加速下滑，由动能定理有：(mgsinα-μmgcosα)L=12mv21④
代入数据得 v1=2m/s⑤
（3）根据牛顿第二定律∑F=ma
有a=g（sinα-μcosα）⑥
代入数据得a=2m/s2
（4）两滑块和弹簧构成的系统在相互作用过程中动量守恒，当它们速度相等时，弹簧具有最大弹性势能，设共同速度为v2，由动量守恒和能量守恒定律有：mv1=（m+m）v2⑦EP=12mv21-12(2m)v22⑧
联立⑤⑦⑧式解得EP=1J．
答：（1）滑块A与斜面的动摩擦因数为0.5．
（2）滑块A到达斜面底端时的速度大小为2m/s．
（3）滑块A在斜面上运动的加速度大小为2m/s2．
（4）弹簧的最大弹性势能为1J．

本题解析：

本题难度：一般

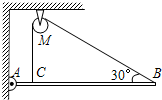
3、选择题  重为60N的均匀直杆AB一端用铰链与墙相连，另一端用一条通过定滑轮M的绳子系住，如图所示，绳子一端与直杆AB的夹角为30°，绳子另一端在C点与AB垂直，AC=0.1AB．滑轮与绳重力不计．求：
（　　）
A．绳对B点的拉力是50N
B．绳对C点的拉力是25N
C．轴对定滑轮M的作用力是75N，方向竖直向上
D．轴对定滑轮M的作用力是50