1、选择题  如图所示，质量为m的物体沿倾 角为θ的斜面匀速下滑，物体与斜面间的动摩擦因数为μ，关于物体在下滑过程中所受滑动摩擦力的大小Ff，下列说法正确的是
①Ff = mgsinθ ②Ff = mgcosθ ③Ff = μmgsinθ ④Ff=μmgcosθ

[? ]

参考答案：D

本题解析：

本题难度：简单

2、计算题  （9分）质量为m=19kg的物体放在水平地面上，物体与地面之间的动摩擦因数为0.25。

（1）如图甲所示，对物体施加一个多大的水平力F1，可使物体在地面上匀速运动？
（2）如图乙所示，如果对物体施加一个与水平方向成37°斜向上的力F2，则F2多大时才可使物体在地面上匀速运动？（已知sin37°=0.6，cos37°=0.8。）

参考答案：（1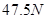）（2）

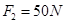
本题解析：（1）要使物体受到水平力F作用时，物体作匀速运动则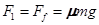?（2分）
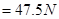?（1分）
（2）将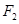分解为水平方向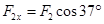?（1分）
竖直方向?（1分）
据力平衡条件知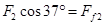：?（2分）
又?（1分）
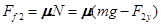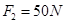可得?（1分）
点评：做此类型的题目时，需先画出受力分析，然后根据力的平衡条件分析

本题难度：一般

3、计算题  如图所示，力F1、F2、F3、F4在同一平面内构成共点力，其中F1=20 N、F2=20 N、F3=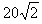N、F4=，各力之间的夹角在图中已标出，求这四个共点力的合力大小和方向。

参考答案：解：本题考查正交分解法的应用，关键是建立合适的坐标系，使各力与坐标轴的夹角为特殊值。以F2方向为x轴的正方向建立坐标系，如图所示，将F1、F3、F4向两坐标轴上分解得：
?
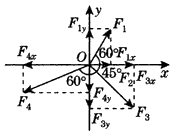F1x=F1cos60°=20×N=10 N
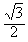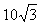F1y=F1sin60°=20×N=N
F2x=20 N，F2y=0
F3x=F3cos45°=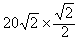N=20 N
F3y=-F3sin45°=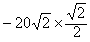N=-20 N
F4x=-F4sin60°=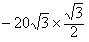N=-30 N
F4y=-F4cos60°=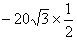N=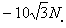
四个力在x方向的合力为Fx=F1x+F2x+F3x+F4x=20 N
在y方向的合力为Fy=F1y+F2y+F3y+F4y=-20 N
四个力的合力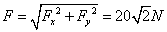，合力方向与F3方向一致

本题解析：

本题难度：一般

4、计算题  如图所示，质量为m的物体处在静止状态。细线OA与竖直方向成30°角，则细线OA、OB的拉力各为多少？

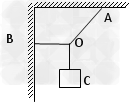
参考答案：解：将物体受力正交分解?
Tcosθ＝mg
Tsinθ＝F?

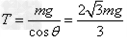
F==?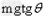

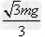
本题解析：

本题难度：一般

5、填空题  如图所示，表面光滑、质量不计的尖劈，插在缝A、B之间，在尖劈背上加一压力F，则尖劈对A侧压力为________，对B侧压力为________。

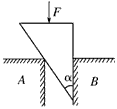
参考答案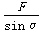：，Fcotα

本题解析：

本题难度：一般