1、选择题 如图所示,甲图中A、B为两个相同的环形线圈,共轴并靠近放置,A线圈中通如图乙所示的交变电流i,则(?)

A. 从t1到t2时间内A、B两线圈吸引
B. 从t2到t3时间内A、B两线圈相斥
C. t1时刻两线圈间作用力为零
D. t2时刻两线圈间的吸引力最大
参考答案:ABC
本题解析:从t1到t2时间内,电流减小,根据楞次定律知吸引,从t2到t3时间内电流增大,根据楞次定律知排斥,AB正确;t1时刻电流最大,但磁场的变化率最小,B线圈中不产生感应电流,无相互作用,t2时刻由于A线圈电流为零,故作用力为零,CD错误
本题难度:简单
2、计算题 如图所示的坐标系,x轴沿水平方向,y轴沿竖直方向。在x轴上方空间的第二象限内,有一个竖直向下的匀强电场;在第三象限,存在沿y轴正方向的匀强电场和垂直xOy平面(纸面)向里的匀强磁场;在第一、第四象限,存在着与x轴正方向夹角为30°的匀强电场,四个象限的电场强度大小均相等。一质量为m、电量为+q的带电质点,从y轴上y=h处的P1点以一定的水平初速度沿x轴负方向进入第二象限,然后经过x轴上x=-2h处的P2的进入第三象限,带电质点恰好能做匀速圆周运动,之后经过y轴上y=-2h处的P3点进入第四象限,已知重力加速为g。求:
(1)粒子到达P2点时速度的大小和方向;
(2)电场强度和磁感应强度的大小;
(3)带电质点在进入第四象限空间运动过程中离x轴最小距离。
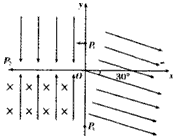
参考答案:解:(1)设第三象限的电场强度大小为E,由粒子进入第三象限恰好能做匀速圆周运动知:

在第二象限,竖直方向加速度
∴水平方向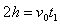 ,竖直方向
,竖直方向
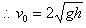 ,
,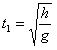
竖直方向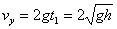
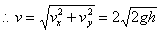
与x轴负向夹角θ,则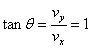
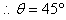
(2)进入第三象限重力和电场力抵消,磁场力提供向心力,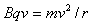
解得: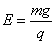 ,
,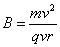
(3)粒子进入第四象限竖直向下的力大小
竖直向下加速度大小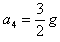
当粒子竖直向上的速度为0时,离x轴最近
即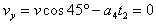
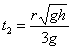
∴粒子上升的最大高度
∴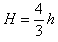
∴离x轴最近的距离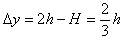
本题解析:
本题难度:困难
3、计算题 在地面上方的真空室内,存在匀强电场和匀强磁场。已知电场强度和磁感应强度的方向是相同的,电场强度的大小E ="4N/c,B=" 0.15T。今有一个带负电的质点以v = 20m/s的速度在此区域内沿垂直于电场强度方向做匀速直线运动,求此带电质点的电量与质量之比q/m以及磁场的所有可能方向。(g=9.8m/s2)
参考答案:由题意可知质点受的重力,电场力和洛伦兹力的合力必为零。由此推知三力在同一竖直平面内,如图所示由平衡条件得
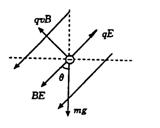
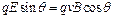
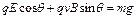
解得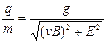 代入数据得:q/m
代入数据得:q/m = 1.96C/kg,?
= 1.96C/kg,?
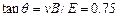 ,所以
,所以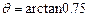 ,
,
即磁场是沿与重力方向成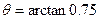 ,且斜向向下的一切方向。
,且斜向向下的一切方向。
本题解析:略
本题难度:简单
4、计算题 如图所示,坐标系xOy在竖直平面内,空间有沿水平方向垂直于纸面向外的匀强磁场,磁感应强度大小为B,在x>0的空间里有沿x轴正方向的匀强电场,场强的大小为E,一个带正电的小球经过图中的x轴上的A点,沿着与水平方向成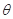 = 300角的斜向下直线做匀速运动,经过y轴上的B点进入x<0的区域,要使小球进入x<0区域后能在竖直面内做匀速圆周运动,需在x<0区域另加一匀强电场,若带电小球做圆周运动通过x轴上的C点,且
= 300角的斜向下直线做匀速运动,经过y轴上的B点进入x<0的区域,要使小球进入x<0区域后能在竖直面内做匀速圆周运动,需在x<0区域另加一匀强电场,若带电小球做圆周运动通过x轴上的C点,且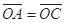 ,设重力加速度为g,
,设重力加速度为g,
求:
(1)小球运动速率的大小;
(2)在x<0的区域所加电场大小和方向;
(3)小球从B点运动到C点所用时间及 的长度.
的长度.
参考答案:(1)  ?(2)
?(2)  ?,方向竖直向上?(3)
?,方向竖直向上?(3) ?、
?、
本题解析:(1)小球从A运动到B的过程中,小球受重力、电场力和洛伦兹力作用而处于平衡状态,
由题设条件知 ,
,
所以小球的运动速率为 。
。
(2)小球在x<0的区域做匀速圆周运动,则小球的重力与所受的电场力平衡,洛伦兹力提供做圆周运动的向心力.
则 ,
,
又 .
.
所以 ,方向竖直向上.
,方向竖直向上.
(3)如图所示,连接BC,过B作AB的垂线交x轴于 .
.

因为 ,所以在
,所以在 中
中 ,又
,又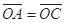 ,故
,故 ,所以
,所以 ,
,  ,则
,则 为小球做圆周运动的圆心.
为小球做圆周运动的圆心.
设小球做圆周运动的半径为R,周期为T,则 ,
,
且 ?
?
 ,
,

由于 ,小球从点B运动到点C的时间为
,小球从点B运动到点C的时间为 ,
,
又∠ BO=300,所以
BO=300,所以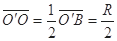 ,
,
所以 ,
,
即
又 ,
,
所以

点评:关键是先确定物体的运动情况,并画出运动轨迹,利用几何知识找圆心和半径,然后逐段逐段分析,匀速运动阶段受力平衡,匀速圆周运动阶段洛伦兹力提供向心力。
本题难度:一般
5、计算题 如图所示,竖直放置的两块很大的平行金属板a、b,相距为d,ab间的电场强度为E,今有一带正电的微粒从a板下缘以初速度v0竖直向上射入电场,当它飞到b板时,速度大小不变,而方向变为水平方向,且刚好从高度也为d的狭缝穿过b板而进入bc区域,bc区域的宽度也为d,所加电场大小为E方向竖直向上,磁感强度方向垂直纸面向里,磁场大小等于E/v0。求:
(1)粒子在ab区域的运动时间?
(2)粒子在bc区域的运动时间?
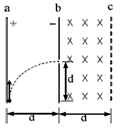
参考答案:解:(1)在ab区域做匀变速曲线运动,水平方向匀加速直线
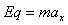 ,
,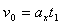 ,
,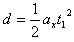
竖直方向匀减速直线
 ,
,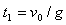 ,
,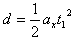 ,
,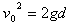
解得: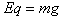 ,
,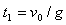 或
或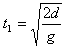
(2)在bc区域 ,
,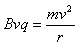 ,所以粒子做匀速圆周运动
,所以粒子做匀速圆周运动
由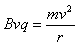 ,
,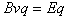 ,
,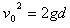
得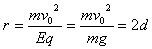
由几何关系得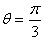
由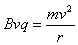 ,
,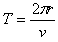 ,
,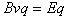 ,
,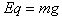
得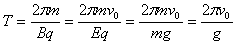
所以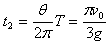 或
或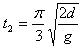
本题解析:
本题难度:困难