1、简答题 如图所示的水平传送装置,AB间距为L,传送带以速度v匀速运转,把一质量为m的零件无初速地放在传送带的A处,已知零件与传送带之间的动摩擦因数为u,试求从A到B的过程中,摩擦力对零件所做的功,和物体与皮带间因摩擦产生的热量Q.
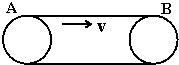
参考答案:要求摩擦力对零件做的功,关键是要弄清零件在摩擦力方向上的位移是多少,由于题中没有给出各物理量之间的定量关系,故存在两种可能.
当零件与传送带之间存在摩擦力时,摩擦力的大小为F=μmg,分两种情况进行讨论:
(1)零件在到达B处时速度小于或刚好等于传送带的速度v,零件在从A到B的过程中一直受摩擦力作用,则摩擦力对零件做功
W=FL=μmgL
设运动时间为t,加速度为a,零件与传送带的相对位移大小为△x,则a=Fm=μg,△x=vt-0+v2t=12vt=L
故Q=F△x=μmgL
(2)零件在到达B点之前已经达到传送带的速度v,零件只是在达到速度v之间的一段时间内受摩擦力作用,此后零件与传送带以相同的速度v做匀速直线运动,不再受摩擦力作用.
则摩擦力对零件所做的功为
W′=FL′=μmgv22μg=12mv2
Q′=W′=12mv2
答:从A到B的过程中,摩擦力对零件所做的功为μmgL或12mv2.物体与皮带间因摩擦产生的热量Q为μmgL或12mv2.
本题解析:
本题难度:一般
2、选择题 如图所示,一木板静止在光滑水平面上,一木块从小车左端开始以速度v沿木板表面滑动。若将木板固定住,滑到木板右端木块克服摩擦力做的功为W1,产生的热量为Q1,运动时间为t1;若木板不固定,滑到木板右端木块克服摩擦阻力做的功为W2,产生的热量为Q2,运动时间为t2则 (?)

A.W1=W2,Q1=Q2 ,t1=t2
B.W1>W2,Q1 >Q2, t1>t2
C.W1<W2,Q1<Q2, t1<t2
D.W1<W2,Q1=Q2, t1<t2
参考答案:D
本题解析:产生的热量等于摩擦力乘相对位移,因为相对位移相等,故两次产生的热量相等Q1=Q2 , 克服摩擦力做的功等于摩擦力乘以对地位移,因为不固定小车对地位移大,所以W1<W2,位移大则运动时间长,即t1<t2,选D
本题难度:简单
3、选择题 细绳一端固定在天花板上,另一端拴一质量为m的小球,如图所示。使小球在竖直平面内摆动,经过一段时间后,小球停止摆动。下列说法中正确的是

A.小球机械能守恒
B.小球能量正在消失
C.小球摆动过程中,只有动能和重力势能在相互转化
D.总能量守恒,但小球的机械能减少
参考答案:D
本题解析:小球在竖直平面内摆动,经过一段时间后,小球停止摆动,说明机械能通过克服阻力做功不断地转化为内能,即机械能不守恒,故A错误;小球的机械能转化为内能,能量的种类变了,但能量不会消失,故B错误;小球长时间摆动过程中,重力势能和动能相互转化的同时,由于阻力的存在,不断地转化为内能,故摆动的幅度越来越小,机械能减小,故C错误,D正确;
故选D.
点评:本题关键是分析清楚小球的能量转化情况,小球短时间摆动,机械能变化很小,可以近似为机械能守恒,长时间摆动,机械能损失不可以忽略不计,故机械能不守恒.
本题难度:一般
4、选择题 水平地面上有两个固定的、高度相同的粗糙斜面甲和乙,乙的斜面倾角大,甲、乙斜面长分别为S、L1,如图所示。两个完全相同的小滑块A、B可视为质点同时由静止开始从甲、乙两个斜面的顶端释放,小滑块A一直沿斜面甲滑到底端C,而小滑块B滑到底端P后沿水平面滑行到D处(小滑块B在P点从斜面滑到水平面的速度大小不变),在水平面上滑行的距离PD=L2,且S=L1+L2。小滑块A、B与两个斜面和水平面间的动摩擦因数相同,则
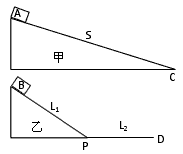
[? ]
A.滑块A到达底端C点时的动能一定比滑块B到达D点时的动能小
B.两个滑块在斜面上加速下滑的过程中,到达同一高度时,动能可能相同
C.A、B两个滑块从斜面顶端分别运动到C、D的过程中,滑块A重力做功的平均功率小于滑块B重力做功的平均功率
D.A、B滑块从斜面顶端分别运动到C、D的过程中,由于克服摩擦而产生的热量一定相同
参考答案:AC
本题解析:
本题难度:一般
5、计算题 如图所示,一固定的楔形木块,其斜面的倾角θ=30°,另一边与地面垂直,顶上有一定滑轮.一柔软的细线跨过定滑轮,两端分别与物块A和B连结,A的质量为4m,B的质量为m,开始时将B按在地面上不动,然后放开手,让A沿斜面下滑而B上升.物块A与斜面间无摩擦.设当A沿斜面下滑S 距离后,细线突然断了.求物块B上升离地的最大高度H. 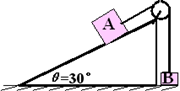
参考答案:
本题解析:对系统由机械能守恒定律

解得: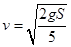
细线断后,B做竖直上抛运动,又上升了 ,由机械能守恒定律
,由机械能守恒定律
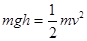 ?得
?得
点评:本题难度较小,处理连接体问题通常利用机械能守恒定律,此题注意两物体上升或下降高度并不想等
本题难度:一般