1、选择题  宇宙间存在一些离其他恒星较远的三星系统，其中有一种三星系统如图所示，三颗质量相等的星球位于等边三角形的三个顶点上，任意两颗星球的距离均为R，并绕其中心O做匀速圆周运动．忽略其他星球对它们的引力作用，引力常量为G，以下对该三星系统的说法正确的是? (　　)．

A．每颗星球做圆周运动的半径都等于R
B．每颗星球做圆周运动的加速度与三颗星球的质量无关
C．每颗星球做圆周运动的周期为T＝2πR
D．每颗星球做圆周运动的线速度v＝2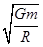

参考答案：C

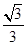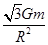本题解析：三颗星球均绕中心做圆周运动，由几何关系可知r＝＝R，A错误；任一星球做圆周运动的向心力由其他两个星球的引力的合力提供，根据平行四边形定则得F＝2cos 30°＝ma，解得a＝，B错误；由F＝2cos 30°＝m＝m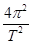r得C正确，D错误．

本题难度：一般

2、选择题  一颗人造卫星以地心为圆心做匀速圆周运动，它的速率、周期跟它的轨道半径的关系（　　?）
A．半径越大，速率越小，周期越大
B．半径越大，速率越大，周期越大　
C．半径越大，速率越小，周期越小
D．半径越大，速率越小，周期不变

参考答案：A

本题解析：由知半径越大，速率越小，B错；由知半径越大，周期越大A对，CD错。

本题难度：一般

3、选择题  人造地球卫星在圆形轨道上环绕地球运行时（?）
A．轨道半径越大，速度越小，周期越长
B．轨道半径越大，速度越大，周期越短
C．轨道半径越大，速度越大，周期越长
D．轨道半径越小，速度越小，周期越长

参考答案：A

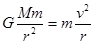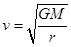本题解析：由公式得,所以轨道半径越大，则速度越小，由公式得，所以轨道半径越大，周期越长，所以选A
考点:万有引力定律的应用
点评：一个天体绕中心天体做圆周运动时万有引力提供向心力，灵活的选择向心力的表达式是我们顺利解决此类题目的基础．我们要按照不同的要求选择不同的公式来进行求解

本题难度：简单

4、计算题  已知地球半径为R，一只静止在赤道上空的热气球（不计气球离地高度）绕地心运动的角速度为ω0，在距地面h高处圆形轨道上有一颗人造地球卫星，设热气球的质量为m，人造地球卫星的质量为m1 ，而地球质量M和万有引力常量G未知。根据上述条件，有一位同学列出了以下两个式子：
对热气球有：GmM/R 2＝mω02R ?
对人造卫星有：Gm1M/（R＋h）2＝m1ω2（R＋h）
进而求出了人造地球卫星绕地球运行的角速度ω．你认为该同学的解法是否正确？若认为正确，请求出结果；若认为错误，请说明理由，并补充一个条件后，再求出ω．

参考答案：错误

本题解析：错误，热气球受到浮力和重力共同作用而处于静止。
方法（1）：设地球表面物体重力加速度g：?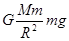
Gm1M/（R＋h）2＝m1ω2（R＋h）
解得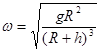：（或）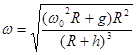
方法（2）：设第一宇宙速度v1：?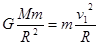
Gm1M/（R＋h）2＝m1ω2（R＋h）
解得：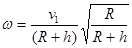
本题考查天体运动知识，热气球受到浮力和重力共同作用而处于静止，不是重力完全充当向心力，所以不能用GmM/R 2＝mω02R

本题难度：一般

5、选择题  某行星的质量是地球的6.4倍，其表面重力加速度是地球表面重力加速度的1.6倍，则该行星的半径与地球的半径之比为（　　）
A．1：1
B．1：2
C．2：I
D．4：1

参考答案：设任一星球的质量为M，半径为R，质量为m的物体在星球表面时，星球对物体的万有引力近似等于物体的重力，则有
? mg=GMmR2
得g=GMR2
所以R=

本题解析：

本题难度：一般