1、实验题  用长度放大600倍的显微镜观察布朗运动，估计放大后的小颗粒(碳)体积为0.1×10-9 m3，碳的密度是2.25×103 kg/m3,摩尔质量是1.2×10-2 kg/mol,阿伏加德罗常数为6.02×1023 mol-1,则该小碳粒含分子数约为__________个(取一位有效数字)，所以布朗运动不是分子运动.

参考答案：5×1010

本题解析：实际碳颗粒的体积为
V=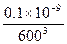?m3
碳颗粒的质量为
m=?kg
碳颗粒的物质的量为
n=?mol
碳颗粒的个数为
N=×6.02×1023个≈5×1010个.

本题难度：简单

2、简答题  已知金刚石的密度是3.5×，摩尔质量M＝.试估算金刚石内碳原子间的平均距离(结果保留两位有效数字)．

参考答案：1.8×

本题解析：
方法一 取质量为1kg的金刚石，根据公式ρ＝m/V得其所占体积为

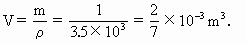
　　由金刚石的摩尔质量M＝得：1kg金刚石中所含碳原子的个数

　　由于固体分子之间的空隙很小，我们可以认为组成金刚石的碳原子是一个挨着一个紧密排列的，因此，每个碳原子所占的体积为

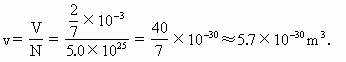
　　将碳原子看成立方体模型，则该立方体的棱长便是碳原子间距离d的平均值，即
　　?≈1.8×．
　　方法二 取体积为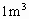的金刚石，根据公式ρ＝m/V得这样一块金刚石的质量
m＝ρV＝3.5×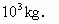
　　由金刚石的摩尔质量M＝12×得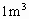(即3.5×)的金刚石中所含碳原子个数为

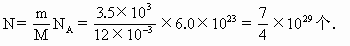
　　一个碳原子所占的体积为
　　v＝V/N＝＝5.7×(认为碳原子一个挨一个紧密排列)．
　　将碳原子看成立方体模型，故碳原子间距离d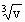＝＝1.8×m．
　　思路点拨：此类估算问题的解题思路是：先设取一定质量的金刚石算出其体积(或设取一定体积的金刚石算出其质量)，再借助摩尔质量和阿伏加德罗常数算出一个碳原子的体积，最后，依据原子模型(球模型或正方体模型)求出原子间的平均距离．
　　小结：本题重点考查解决估算问题的能力．解决这类问题离不开下面的三个假设与近似：其一，设固体分子一个挨着一个紧密排列(即假设固体分子间没有空隙)；其二，假设分子模型为立方体模型，这种假设可以简化运算，本题若将原子按球模型处理，则根据公式


即分子间的平均距离为2.2×，与按照立方体模型估算的结果非常接近；其三，在求的值时，采用“试幂法”，即倒着算．

本题难度：简单

3、选择题  已知某气体的摩尔体积为VA，摩尔质量为MA，阿伏加德罗常数为NA，则根据以上数据可以估算出的物理量是                                                  (　　)
A．分子质量
B．分子体积
C．分子密度
D．分子间平均距离