1、选择题 已知一个氢原子的质量为1.6736×10-27 kg,一个锂原子的质量为11.6505×10-27 kg,一个氦原子的质量为6.6467×10-27 kg。一个锂核受到一个质子轰击变为2个α粒子,核反应方程为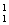 H+
H+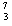 Li →2
Li →2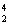 He。根据以上信息,以下判断正确的是
He。根据以上信息,以下判断正确的是
[? ]
A.题中所给的核反应属于α衰变
B.题中所给的核反应属于轻核聚变
C.根据题中信息,可以计算核反应释放的核能
D.因为题中给出的是三种原子的质量,没有给出核的质量,故无法计算核反应释放的核能
参考答案:C
本题解析:
本题难度:一般
2、填空题 镭核(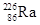 )经过一系列α衰变和β衰变,变成铅核(
)经过一系列α衰变和β衰变,变成铅核(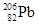 ) ,其中经过α衰变的次数是_____,镭核(
) ,其中经过α衰变的次数是_____,镭核(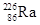 )衰变成铅核(
)衰变成铅核(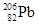 )的过程中损失了_______个中子.
)的过程中损失了_______个中子.
参考答案:5,6
本题解析:每次α衰变质量数减少4,每次β衰变质量数不变,所以226-206则质量数减少4,即等效5次α衰变,同时质子数减少10,即此刻应该为86-10=76.每次β衰变,质子数增加1,即82-76=6次β衰变。
点评:本题考查了核反应方程的配平方法:保持质量数和电荷数守恒。
本题难度:简单
3、选择题 在下列两个核反应方程中,X1、X2分别代表一种粒子。 ①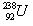 →
→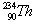 ﹢X1;②
﹢X1;② ﹢
﹢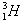 →
→ ﹢X2,以下判断中正确的是
﹢X2,以下判断中正确的是
[? ]
A.①是重核裂变反应
B.②是轻核聚变反应
C.X1是α粒子,此种粒子形成的射线具有很强的贯穿本领
D.X2是中子,X2的质量等于 与
与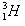 质量之和减去
质量之和减去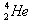 的质量
的质量
参考答案:B
本题解析:
本题难度:简单
4、计算题 在β衰变中常伴有一种称为“中微子”的粒子放出,中微子的性质十分特别,因此在实验中很难探测。1953年,莱尼斯和柯文建造了一个由大水槽和探测器组成的实验系统,利用中微子与水中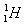 的核反应,间接地证实了中微子的存在。
的核反应,间接地证实了中微子的存在。
(1)中微子与水中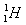 的发生核反应,产生中子(
的发生核反应,产生中子(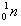 )和正电子(
)和正电子(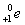 ),即中微子
),即中微子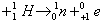 。可以判定,中微子的质量数和电荷数分别是__________。
。可以判定,中微子的质量数和电荷数分别是__________。
A.0和0
B.0和1
C.1和0
D.1和1
(2)上述核反应产生的正电子与水中的电子相遇,与电子形成几乎静止的整体后,可以转变为两个光子(γ),即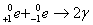 。已知正电子和电子的质量都为9.1×10-31 kg,反应中产生的每个光子的能量约为__________J。正电子与电子相遇不可能只转变为一个光子,原因是_____________________。
。已知正电子和电子的质量都为9.1×10-31 kg,反应中产生的每个光子的能量约为__________J。正电子与电子相遇不可能只转变为一个光子,原因是_____________________。
(3)试通过分析比较,具有相同动能的中子和电子的物质波波长的大小。
参考答案:解:(1)A
(2)8.2×10-14,遵循动量守恒
(3)粒子的动量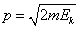
物质波的波长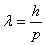
由mn>me,知pn>pe,则λn<λe
本题解析:
本题难度:一般
5、填空题 轻核聚变比重核裂变能够释放更多的能量,若实现受控核聚变,且稳定地输出聚变能,人类将不再有“能源危机”。一个氘核(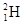 )和一个氚核(
)和一个氚核(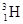 )聚变成一个新核并放出一个中子(
)聚变成一个新核并放出一个中子(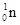 )。
)。
①完成上述核聚变方程 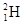 +
+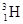 →?+
→?+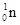
②已知上述核聚变中质量亏损为 ,真空中光速为c,则该核反应中所释放的能量为
,真空中光速为c,则该核反应中所释放的能量为
?。
参考答案:① 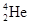 ?(2分)? ②
?(2分)? ② 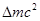
本题解析:①根据质量数,质子数守恒可得: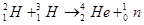
②根据质能方程可得: 
点评:在书写核反应方程时一定要注意电荷数,质量数守恒
本题难度:一般