1、选择题  在静止的电梯里放一桶水，把一个轻弹簧的一端连在桶底，另一端连接在浸没在水中的质量为m的软木塞上，轻弹簧处于伸长状态，如图所示．当电梯由静止开始匀加速下降（a<g）时，轻弹簧的长度将发生怎样的变化：

A.伸长量保持不变
B.由伸长变为压缩
C.伸长量增加
D.伸长量减小

参考答案：D

本题解析：电梯静止时，软木塞受到弹簧的支持力N1，自身的重力G以及浮力F，且G-N1-F=0，得N1=G-F；当电梯加速向下运动时，软木塞受到的弹簧支持力N2，且G-N2-F=ma，得N2=G-F-ma，所以N2<N1，弹簧的形变量变小。选D

本题难度：简单

2、选择题  如图所示，在质量为M的小车中，用细线悬挂一个质量为m的小球，在水平牵引力F的作用下，小车向右做匀加速运动，稳定时悬绳向左偏转的角度为α，撤去牵引力F后，小车继续向右运动过程，稳定时小球向右偏转的角度为β．牵引力F的大小是
A.Mgtanα
B.（M+m）gtanα
C.Mg（tanα+tanβ）
D.（M+m）g（tanα+tanβ）

参考答案：D

本题解析：分析：小球与小车相对静止时具有相同的加速度，根据两次相对静止的情况，根据受力分析，求出加速度的大小，再对整体分析，根据牛顿第二定律求出牵引力的大小．
解答：小球受重力和拉力，稳定时悬绳向左偏转的角度为α时，小球的加速度a1=gtanα．方向水平向右；
稳定时小球向右偏转的角度为β时，小球的加速度a2=gtanβ，方向水平向左．小球与小车具有相同的加速度．
对整体分析有：F-f=（M+m）a2，f=（M+m）a2，联立两式解得：F=（M+m）g（tanα+tanβ）．故D正确，A、B、C错误．
故选D．
点评：解决本题的关键综合运用了整体法和隔离法，知道小球和车具有相同的加速度．

本题难度：一般

3、选择题  质量不等但有相同动能的两物体，在动摩擦因数相同的水平地面上滑行直到停止，则
A.质量大的物体滑行距离小
B.它们滑行的距离一样大
C.质量大的物体滑行时间短
D.它们克服摩擦力所做的功不一样多

参考答案：B

本题解析：本题考查动能的概念、牛顿第二定律的应用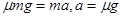，，两物体加速度相同，由v=at，动能相同质量不同，速度则不同，运动时间不同，质量大的速度小，由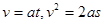，B对，克服摩擦力所做的功等于物体动能的减小量，所以客服摩擦力做功相同，D错

本题难度：困难

4、选择题  下列哪组单位与m/s2等价
A.N/kg
B.N/m
C.N/s
D.J/m

参考答案：A

本题解析：分析：根据加速度a与其他量的关系，推导单位关系．
解答：m/s2是加速度的单位．
根据a=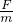得：
1m/s2=1N/kg
故选A．
点评：物理规律不仅反映了物理量的数量关系，也反映它们之间的单位关系，熟知各个物理量的单位以及物理量之间关系公式，就正确解答本题．

本题难度：简单

5、选择题 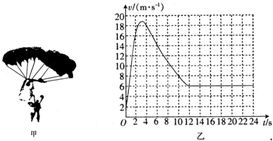 如图甲所示中，总质量为80kg的跳伞运动员从离地500m高处开始跳伞，经过2s拉开绳索开启降落伞，乙图是运动员跳伞过程中的v-t图象，由图象可知（g=10m/s2）、
A.在t=1s时运动员的加速度约为7m/s2
B.14s内运动员下落高度约为266m
C.运动员落地前运动时间为36s
D.运动员在下降过程中空气阻力一直在增大

参考答案：A

本题解析：分析：首先分析运动员的运动情况，运动员在0-2s内做匀加速直线运动，2s-14s做变加速运动，14s以后做匀速运动直到地面．t=1s时运动员做匀加速直线运动，根据图象可以算出a，根据牛顿第二定律算出f，可以通过图象与时间轴所围成的面积估算14s内运动员下落的高度．
解答：A、运动员在0-2s内做匀加速直线运动，图象的斜率表示加速度，所以t=1s时运动员的加速度大小为：
a==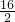m/s2=8m/s2，估算时可以存在一定的偏差，故A正确；
B、面积可以通过图象与时间轴所围成的面积估算，本题可以通过数方格的个数来估算，（大半格和小半格合起来算一格，两个半格算一格）每格面积为4m2，
14s内数得的格数大约为40格，所以14s内运动员下落的高度为：h=40×2×2m=160m，故B错误；
C、14s末的速度为：v=6m/s
14s后做匀速运动，时间t=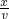=s=57s
所以运动员落地前飞行时间为：14+57s=71s，故C错误；
D、运动员在下降过程中加速度是变化的，运动员受重力和空气阻力，重力恒定，故阻力是变化的，故D错误；
故选A．
点评：该题是v-t图象应用的典型题型，斜率表示加速度，图象与坐标轴围成的面积表示位移，有方格时，面积可以通过数方格的个数来估算．

本题难度：困难