1、简答题  竖直放置的平行金属导轨上端连接一电阻R，质量为m的金属棒与导轨接触良好，并能无摩擦下滑．在金属棒的下方有一垂直于纸面向里的磁感应强度为B的匀强磁场，磁场上边界距金属棒的高度为H，如图所示．把金属棒由静止释放，金属棒在磁场中的运动情况如何？（金属棒与导轨的电阻不计，两平行导轨的间距为L）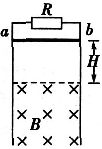

参考答案：金属棒从静止释放后先做自由落体运动，下落的高度为 H时的速度：v=

本题解析：

本题难度：一般

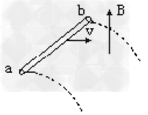
2、选择题  金属杆ab水平放置在某高处，当它被平抛进入方向坚直向上的匀强磁场中时(如图所示)，以下说法中正确的是

[? ]
A．运动过程中感应电动势大小不变，且Ua＞Ub
B．运动过程中感应电动势大小不变，且Ua＜Ub
C．由于速率不断增大，所以感应电动势不断变大，且Ua＞Ub
D．由于速率不断增大，所以感应电动势不断变大，且Ua＜Ub

参考答案：A

本题解析：

本题难度：一般

3、选择题  关于电磁感应现象，下列说法不正确的是
A奥斯特发现电流的磁效应，激发了法拉第对对电磁感应现象的研究
B感应电动势的大小与回路中的磁通量成正比
C俄国物理学家楞次找到了判断感应电流方向的方法
D法拉第电磁感应定律可用来确定感应电动势大小

参考答案：B

本题解析：由教材可知，奥斯特发现电流的磁效应，激发了法拉第对对电磁感应现象的研究，A错；由法拉第电磁感应定律知感应电动势的大小与回路中的磁通量的变化率成正比，B对；俄国物理学家楞次总结了楞次定律可判断感应电流方向，C错；由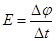知法拉第电磁感应定律可用来确定感应电动势大小，D错。

本题难度：简单

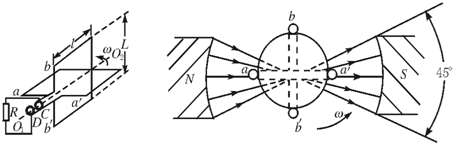
4、简答题  如图左所示，边长为l和L的矩形线框aa′、bb′互相垂直，彼此绝缘，可绕中心轴O1O2转动，将两线框的始端并在一起接到滑环C，末端并在一起接到滑环D，C、D彼此绝缘．通过电刷跟C、D连接．线框处于磁铁和圆柱形铁芯之间的磁场中，磁场边缘中心的张角为45°，如图右所示（图中的圆表示圆柱形铁芯，它使磁铁和铁芯之间的磁场沿半径方向，如图箭头所示）．不论线框转到磁场中的什么位置，磁场的方向总是沿着线框平面．磁场中长为l的线框边所在处的磁感应强度大小恒为B，设线框aa′和bb′的电阻都是r，两个线框以角速度ω逆时针匀速转动，电阻R=2r．
（1）求线框aa′转到图右位置时感应电动势的大小；
（2）求转动过程中电阻R上的电压最大值；
（3）从线框aa′进入磁场开始，作出0～T（T是线框转动周期）时间内通过R的电流iR随时间变化的图象；
（4）求外力驱动两线框转动一周所做的功．

参考答案：

（1）由题，线框转到磁场中的任何位置时，磁场的方向总是沿着线框平面，则线框切线感线的速度方向始终与磁感线垂直，则感应电动势的大小E=2Blv=2BlωL2=BlLω．
（2）线框转动过程中，只有一个线框进入磁场切割磁感线作为电源，另一个线框与外接电阻R并联后作为外电路，则电源的内阻为r，外电路总电阻为R外=RrR+r=23r，故R两端的电压最大值为：
? UR=IR外=Er+23r?23r=25BlLω
（3）aa′和bb′在磁场中，通过R的电流大小相等，
? iR=URR=25BlLω?12r=BlLω5r．
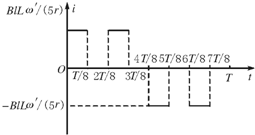
从线框aa′进入磁场开始，每转45°，即T8周期时间，电流发生一次变化，作出电流的图象如图所示．
（4）每个线框作为电源时，电路中总电流为：
? I=ER外+r=E23r+r=3E5r，提供的总功率为P=EI=3E25r=3(BlLω)25r
根据能量转化和守恒定律得：
? W外=4P?T8=P?T2=P?πω=3πB2l2L2ω5r
答：（1）线框aa′转到图右位置时感应电动势的大小为BlLω．；
（2）转动过程中电阻R上的电压最大值25BlLω；
（3）从线框aa′进入磁场开始，在0～T时间内通过R的电流iR随时间变化的图象如图所示；
（4）外力驱动两线框转动一周所做的功为3πB2l2L2ω5r．

本题解析：

本题难度：一般

5、选择题  如图所示，在光滑绝缘的水平桌面上放一弹性闭合导体环，在导体环轴线上方有一条形磁铁．当条形磁铁沿轴线竖直向下迅速移动时，下列判断中正确的是（　　）
A．导体环有收缩趋势
B．导体环有扩张趋势
C．导体环对桌面压力减小
D．导体环对桌面压力增大