1、选择题  在建筑工地上有时需要将一些建筑材料由高处送到低处，为此工人们设计了一种如图所示的简易滑轨：两根圆柱形木杆AB和CD相互平行，斜靠在竖直墙壁上，把一摞瓦放在两木杆构成的滑轨上，瓦将沿滑轨滑到低处。在实际操作中发现瓦滑到底端时速度较大，有可能摔碎，为了防止瓦被损坏，下列措施中可行的是

[? ]
A．增大两杆之间的距离
B．减小两杆之间的距离
C．减少每次运送瓦的块数
D．增多每次运送瓦的块数

参考答案：A

本题解析：

本题难度：一般

2、计算题  （12分）如图所示，光滑水平面上静止放着长L=1.6m，质量为M=3kg的木板，一个质量为m=1kg的小物块放在木板的最右端，m与M之间的动摩擦因数为μ="0.1" ，现对木板施加一个水平向右的拉力F。（小物块可看作质点，g=10m/s2）

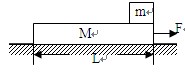
（1）施加F后，要想把木板从物体m的下方抽出来，求力F的大小应满足的条件；
(2)如果所施力F="10" N，为了把木板从物体的下方抽出来，此力F的作用时间不得小于多少？

参考答案：（1）F>(M＋m) am＝4N（2）t=0.8s

本题解析：力F作用在木板上时，m的加速度为am,M的加速度为aM，F至少作用时间为t
(1)am＝μg＝1m/s2?
F>(M＋m) am＝4N
（2）am＝μg＝1m/s2
aM＝（F－μmg）/M＝3m/s2
作用t时间后撤去力F时两者速度分别为Vm，VM，位移分别为Sm，SM
Vm＝t? VM＝3t
Sm＝Vm t/2? SM＝VM t/2
ΔS1＝SM－Sm＝t2
设撤去力F后最后的共同速度为V ，相对滑动位移为ΔS2
t=0.8s
点评：做此类问题，需要根据题中的信息，找出临界条件，然后结合牛顿第二定律解题

本题难度：一般

3、选择题  竖直起飞的火箭在推力F的作用下产生10m/s2的加速度，若推动力增大到2F，则火箭的加速度将达到（g取10m/s2，不计空气阻力）(? )
A．20m/s2
B．25m/s2
C．30m/s2
D．40m/s2

参考答案：C

本题解析：根据牛顿第二定律可知，当推力为2F有，代入数据解得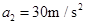，所以只有C正确。

本题难度：简单

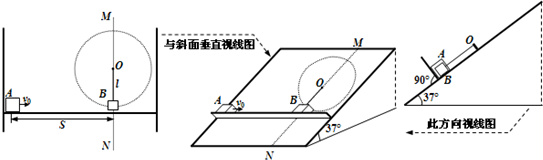
4、简答题  如图所示，倾角为37°的足够大斜面以直线MN为界由两部分组成，MN垂直于斜面水平底边PQ且其左边光滑右边粗糙，斜面上固定一个既垂直于斜面又垂直于MN的粗糙挡板．质量为m1=3kg的小物块A置于挡板与斜面间，A与挡板间的动摩擦因数为μ1=0.1．质量为m2=1kg的小物块B用不可伸长的细线悬挂在界线MN上的O点，细线长为l=0.5m，此时，细线恰好处于伸直状态．A、B可视为质点且与斜面粗糙部分的动摩擦因数均为μ2=0.3，它们的水平距离S=7.5m．现A以水平初速v0=5m/s向右滑动并恰能与B发生弹性正撞．g=10m/s2．求：
（1）A碰撞前向右滑动时受到的摩擦力；
（2）碰后A滑行的位移；
（3）B沿斜面做圆周运动到最高点的速度．

参考答案：
（1）分析物块A的受力得：f=μ1m1gsin37°=0.1×3×10×0.6=1.8（N）
（2）设A运动至与B相碰前速度为?v1，由动能定理得：
? -μ1m1gsin370?s=12m1v21-12m1v20
解得：v1=4m/s
A和B发生弹性正碰，由动量守恒和能量守恒得：
? m1v1=m1v"1+m2v2
? 12m1v21=12m1v′21+12m2v22
解得：v"1=2m/s? v2=6m/s
设A滑行的位移为s1，由动能定理得：
-(μ2m1gcos37°+μ1m1gsin37°)s1=0-12m1v′21
解得：s1=23m≈0.67m
（3）设B做圆周运动到最高点的速度为v3，
由动能定理得：-μ2m2gcos37°πl-m2gsin37°?2l=12m2v23-12m2v22
代入解得? v3≈4.1m/s



答：
（1）A碰撞前向右滑动时受到的摩擦力1.8N；
（2）碰后A滑行的位移为0.67m；
（3）B沿斜面做圆周运动到最高点的速度为4.1m/s．

本题解析：

本题难度：一般

5、简答题  一个倾角为θ=37°的斜面固定在水平面上，一个质量为m=1.0kg的小物块（可视为质点）以v0=4.0m/s的初速度由底端沿斜面上滑，小物块与斜面的动摩擦因数μ=0.25．若斜面足够长，已知sin37°=0.6，cos37°=0.8，g取10m/s2，求：
（1）小物块沿斜面上滑时的加速度大小；
（2）小物块上滑的最大距离；
（3）小物块返回斜面底端时的速度大小．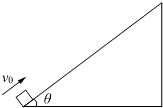

参考答案：（1）小物块在斜面上的受力情况如右图所示，重力的分力

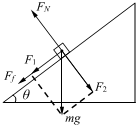
本题解析：

本题难度：一般