1、填空题  水平地面上斜放着一块木板，木板上放着一个质量为m的木块，木块与木板间的动摩擦因数为μ，如图所示。当木板与水平面间的夹角为α（较小角）时，木块静止在木板上，则此时木块受到的摩擦力大小为________；当木板与水平面间的夹角为β（较大角）时，木块沿木板下滑，则此时木块受到的摩擦力大小为________。

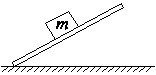
参考答案：mgsinα，μmgcosβ

本题解析：

本题难度：一般

2、简答题  如图一所示，ABCD是一个T型支架，已知整个支架的质量为m1=5kg，质心在BD上、离B点0.2m的O点处，BD=0.6m，D点通过铰链连接在水平地面上，ABC部分成为一斜面，与水平地面间的夹角为37°，且AB=BC．现有一质量为m2=10kg的钢块以v=4m/s的初速度滑上ABC斜面，钢块与斜面间的动摩擦因数μ=0.25．问：T型支架会不会绕D点转动？

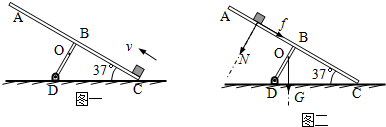
某同学的解题思路如下：
可以先算出钢块静止在ABC上恰好使支架转动的位置，如图二所示．根据支架受力情况写出此时力矩平衡的式子：MN=Mf+MG，可根据该式子求出该位置到C点的距离S1；
（?MN、Mf、MG分别是钢块对斜面的压力的力矩、摩擦力的力矩以及T型支架自身重力的力矩，其中N=m2gcos37°，f=m2gsin37°．）
然后算出钢块以4m/s的速度在斜面上最多能滑行的距离S2；
比较这两个距离：若S1≥S2，则T型支架不会绕D点转动；若S1＜S2，则会转动．
请判断该同学的解题思路是否正确，若正确，请按照该思路，写出详细的解题过程，求出结果；若不正确，请给出你认为的正确解法．

参考答案：该同学的思路中有一些错误．?
钢块在斜面上运动时，对斜面产生的摩擦力是滑动摩擦力，方向沿斜面向上，恰好转动时的力矩平衡的表达式应该是：
? MN+Mf=MG
m2gcos37°×（S1-0.8）+μm2gcos37°×0.6=m1g×0.4sin37°?
可解出S1=0.8m，
另外，钢块沿斜面向上滑动的加速度为a=mgsin37°+μmgcos37°m=gsin37°+μgcos37°=8m/s2，
若斜面固定钢块最多能滑行的距离S2=v22a=1.0m，则?S1＜S2，所以T型支架会绕D点转动．?
答：该同学的思路中有一些错误．T型支架会绕D点转动．

本题解析：

本题难度：一般

3、选择题  如图所示，质量为m的工件置于水平放置的钢板C上，二者间的动摩擦因数为μ，由于光滑导槽A，B的控制，工件只能沿水平导槽运动，现在使钢板以速度v1向右运动，同时用力F拉动工件（F方向与钢板平行）使其以速度v2沿导槽运动，则摩擦力的大小为

[? ]
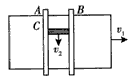
A．等于μmg
B．大于μmg
C．小于μmg
D．等于F

参考答案：解：工件有相对于钢板水平向左的速度v1和沿导槽的速度v2，故工件相对于钢板的速度如图所示，滑动摩擦力方向与相对运动方向相反，

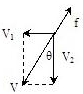
所以有： f=μmg 故选A．

本题解析：

本题难度：简单

4、计算题  风动实验室中可产生水平方向的、大小可调节的风力，现将一套有小球的细直杆放入风洞实验室。小球孔径略大于细杆直径，如图所示。
（1）当杆在水平方向上固定时，调节风力的大小，使小球在杆上做匀速运动，这时小球所受风力的大小为小球所受重力的0.5倍，求小球与杆间的动摩擦因数。
（2）保持小球所受风力不变，使杆与水平方向间夹角为37°并固定，则小球从静止出发在细杆上滑下距离s所需的时间为多少？（0.6，0.8）

参考答案：解：（1）设小球所受的风力为F，小球质量为m，杆对小球的摩擦力为f
? 依题意有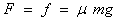
? 所以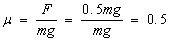
（2）设杆对小球的支持力为N，摩擦力为f，如下图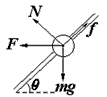：? ? 沿杆方向有 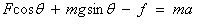①
? 垂直于杆方向有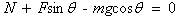 ②
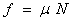? 又 ③
? 三式联立，求得?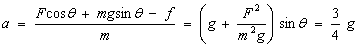
?
?
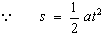
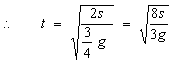
答：（1）动摩擦因数为0.5；（2）所需时间为。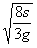

本题解析：

本题难度：困难

5、简答题  

Ⅰ．某同学做探究“合力的功和物体速度变化关系”的实验装置如图1，小车在橡皮筋作用下弹出，沿木板滑行．用一条橡皮筋时对小车做的功记为W，当用2条、3条…，完全相同的橡皮筋并在一起进行第2次、第3次…实验时，每次实验中橡皮筋伸长的长度都保持一致．实验中小车获得的速度由打点计时器所打的纸带测出．实验中木板水平放置，小车在橡皮筋作用下运动，当小车速度最大时，关于橡皮筋所处的状态与小车所在的位置，下列说法正确的是______
A．橡皮筋仍处于伸长状态
B．橡皮筋恰好恢复原长
C．小车恰好运动到两个铁钉的连线处
D．小车已超过两个铁钉的连线
Ⅱ．探究能力是物理学研究的重要能力之一，有同学通过设计实验探究绕轴转动而具有的转动动能与哪些因素有关．他以圆形砂轮为研究对象，研究其转动动能与质量、半径、角速度的具体关系．砂轮由动力带动匀速旋转测得其角速度ω，然后让砂轮脱离动力，用一把弹性尺子与砂轮接触使砂轮慢慢停下，设尺子与砂轮间的摩擦力大小恒为

参考答案：Ⅰ（1）平衡摩擦力后，橡皮筋的拉力等于合力，橡皮条做功完毕，小车的速度最大，若不进行平衡摩擦力操作，则当橡皮筋的拉力等于摩擦力时，速度最大，本题中木板水平放置，显然没有进行平衡摩擦力的操作，因此当小车的速度最大时，橡皮筋仍处于伸长状态，故BCD错误，A正确．
Ⅱ（1）砂轮停下时，砂轮边缘某点转过的弧长s=2πn，其中n是砂轮转过的圈数，砂轮克服摩擦力做的功等于砂轮动能的变化量，由能量守恒率可知：EK=Wf=fs=10π×2πn=20n（cm）=0.2n（m），实验时砂轮的动能如下表所示：
半径r/cm质量/m0角速度（rad/s）圈数转动动能/J41281.60413183.60414326.40422163.20432244.80442326.40812163.201212244.801612326.40①根据第一、二、三组数据，半径、质量相同，角速度不同，发现角速度变为原来的2倍，转动动能变为原来的4倍，角速度变为原来的32倍，转动动能变为原来的94倍，可知转动动能与角速度的二次方成正比．②根据第一、四组数据，半径、角速度相同，质量不同，发现质量变为原来的2倍，转动动能变为原来的2倍，可知转动动能与质量成正比．③由第七九两组数据可知，质量、角速度相同，半径不同，发现半径变为原来的2倍，转动动能变为原来的2倍，可知转动动能与半径的成正比，综上所述，转动动能与质量、半径成正比、与角速度的二次方成正比，表达式为：
EK=kmω2r（k为比例系数）；
（2）分析的过程中总要控制一些量不变，故答案为：控制变量法．
Ⅲ：（1）应调整定滑轮高度，使细线与长木板平行．
（2）对木块、砝码盘和砝码组成的系统，
由牛顿第二定律得：mg-μMg=（M+m）a，
解得：μ=mg-(m+M)aMg；
（3）相邻两计数点间还有4个打点未画出，所以相邻的计数点之间的时间间隔为0.1s，
根据运动学公式得：△x=at2，a=(x5-x1)+(x6-x2)8t2≈1.3m/s2．
故答案为：Ⅰ、A；Ⅱ、（1）kmω2r；（2）控制变量法；
Ⅲ．（1）细线与长木板平行；（2）mg-(m+M)aMg；（3）1.3．

本题解析：

本题难度：一般