1、选择题  如图所示，物体受水平力F作用，物体和放在水平面上的斜面都处于静止，若水平力F增大一些，整个装置仍处于静止，则：

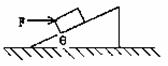
A．斜面对物体的弹力一定增大；
B．斜面与物体间的摩擦力一定增大；
C．水平面对斜面的摩擦力不一定增大；
D．水平面对斜面的弹力一定增大；

参考答案：A

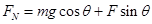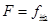本题解析：对木块受力分析，可求得斜面对物体的弹力为 ，所以若水平力F增大一些，斜面对物体的弹力一定增大；若开始时斜面给物体间的摩擦力向上，即，则随F的增大，f会减小；对木块和斜面的整体，水平方向满足，所以随F的增大，会增大；竖直方向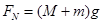，所以随F的增大，FN不变。选项A正确。

本题难度：一般

2、选择题  如图所示，倾角为q的斜面上固定有一竖直挡板，重为G的光滑小球静止时，挡板对球的弹力大小为FN1，斜面对球的弹力大小为FN2，则（?）

A．FN1＝Gtanq
B．FN1＝Gsinq
C．FN2＝Gcosq
D．FN2＝Gsinq

参考答案：A

本题解析：挡板对球的弹力大小为FN1＝Gtanq，A对，B错
斜面对球的弹力大小为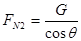，CD错

本题难度：简单

3、计算题  （10分）如图所示，一质量m=2.6kg的木块置于水平地面上，当用与水平方向成θ=370夹角的拉力F=10N拉木块时，木块做匀速直线运动。

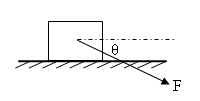
（1）对木块受力分析，画出力的示意图，并建立直角坐标分解拉力F；
（2）求木块受到的支持力N和摩擦力f；
（3）如果撤去拉力F，当木块处于静止时，分别改用水平拉力F1=2N，F2=7N拉木块时，求木块受到的摩擦力大小各是多少。（g="10" m/s2，设最大静摩擦力等于滑动摩擦力）

参考答案：（1）（2）（3）

本题解析：（1）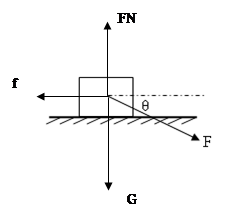
（2）



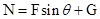
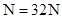
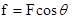
(3)


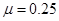
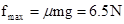
当F1=2N，?，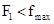
当F2=7N，，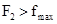
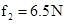
点评：此类题型考察了对于物体的受力分析、通过正交分解法求静摩擦力的方法。

本题难度：一般

4、选择题  如图所示,轻弹簧两端拴接两个小球a、b,拴接小球的细线固定在天花板,两球静止,两细线与水平方向的夹角α=30°,弹簧水平,以下说法正确的是(　　)

A．两球质量一定相等
B．两球质量可能不相等
C．剪断左侧细线瞬间,a球加速度为g
D．剪断左侧细线瞬间,b球加速度为g

参考答案：A

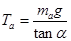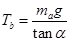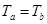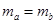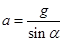本题解析：对a分析可得，对b分析可得 ，根据牛顿第三定律的，所以可得，A正确，B错误；剪断左侧细线的同时，由于弹簧来不及改变，所以b的加速度仍为零，D错误；a所受的细线的拉力为零，弹簧的拉力与重力的合力等于细线的拉力，所以细线的拉力,故加速度，C错误

本题难度：一般

5、选择题  如图，质量分别为mA和mB的两小球带有同种电荷，电荷量分别为qA和qB，用绝缘细线悬挂在天花板上，平衡时，两小球恰处于同一水平位置，细线与竖直方向间夹角分别为θ1与θ2(θ1＞θ2)，两小球突然失去各自所带电荷后开始摆动，最大速度分别为vA和vB，最大动能分别为EkA和EkB，则(? )

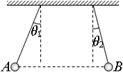
A．qA一定小于qB
B．mA一定小于mB
C．vA一定大于vB
D．EkA一定大于EkB

参考答案：BCD

本题解析：对小球，均受重力mg和水平库仑力F和细线的拉力T，根据平衡条件可知：F＝mgtanθ，根据牛顿第三定律可知FA＝FB，又因为θ1＞θ2，所以有mA＜mB，与电量q无关，故选项A错误；选项B正确；当两球所带电荷突然失去后，库仑力突然消失，两球将分别绕悬点摆动，摆动过程中只有各自的重力做功，以开始时两球的水平连线所在水平面为零势能面，则有EA＝EB，根据机械能守恒定律可知，摆到最低点时速度最大，动能亦最大，有：mgl(1－cosθ)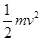＝，解得：v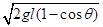＝，根据图中几何关系可知：lAcosθ1＝lBcosθ2，结合θ1＞θ2，可以判断出lA＞lB，有vA＞vB，故选项C正确；Ek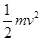＝＝mgl(1－cosθ)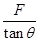＝l(1－cosθ)＝Flcosθ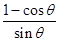＝Flcosθtan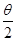，显然有：FAlAcosθ1＝FBlBcosθ2、tan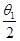＞tan，所以有：EkA＞EkB，故选项D正确。

本题难度：一般