1、计算题 如图所示,甲车的质量是2 kg,静止在光滑水平面上,上表面光滑,右端放一个质量为1 kg的小物体.乙车质量为4 kg,以5 m/s的速度向左运动,与甲车碰撞以后甲车获得8 m/s的速度,物体滑到乙车上.若乙车足够长,上表面与物体的动摩擦因数为0.2,则物体在乙车上表面滑行多长时间相对乙车静止?(g取10 m/s2)

参考答案:0.4 s
本题解析:乙与甲碰撞动量守恒:m乙v乙=m乙v乙′+m甲v甲′
小物体m在乙上滑动至有共同速度v,对小物体与乙车运用动量守恒定律得:
m乙v乙′=(m+m乙)v,
对小物体应用牛顿第二定律得? a=μg
所以? t= ,
,
代入数据得? t="0.4" s。
点评:本题考察了相互作用力的物体的动量守恒定律的运用和理解。
本题难度:一般
2、计算题 如图所示,木块A的右侧为光滑曲面,且下端极薄,其质量为mA=2.0
参考答案:
本题解析:
本题难度:一般
3、简答题 在光滑的水平面上沿直线按不同的间距依次排列着质量均为m的滑块,1、2、3、…(n-1)、n,滑块P的质量也为m.P从静止开始在大小为F的水平恒力作用下向右运动,经时间T与滑块1碰撞,碰撞后滑块便粘连在一起.以后每经过时间T就与下一滑块碰撞一次,每次碰撞后均粘连在一起,每次碰撞时间极短,每个物块都可简化为质点.求:
?
(1)第一次碰撞后瞬间的速度及第一次碰撞过程中产生的内能;
(2)发生第n次碰撞后瞬间的速度vn为多大;
(3)第n-1个滑块与第n个滑块间的距离sn-1.
参考答案:(1)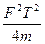 ;(2)
;(2)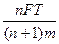 ;(3)
;(3)
本题解析:(1)设第一次碰撞前瞬间P的速度为u1,根据动量定理,有
FT=mu1?①
则撞前瞬间的速度u1= ? ②
? ②
因碰撞时间极短,第一次碰撞后瞬间的速度为v1,根据动量定理,有
FT=2mv1? ③
则碰后瞬间速度v1= ? ④
? ④
第一次碰撞过程中产生的内能△E=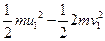 =
=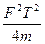 ? ⑤
? ⑤
(2)因每次碰撞时间极短,对从开始到发生第n次碰撞后瞬间应用动量定理,有
FnT=(n+1)mvn? ⑥
解得vn=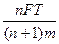 ? ⑦
? ⑦
(3)同理可以求出第(n-1)次碰后的速度vn-1=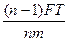 ? ⑧
? ⑧
对第n次碰撞前全过程应用动量定理
FnT=nmun? ⑨
解得un= ? ⑩(与n无关)
? ⑩(与n无关)
对n-1到n之间应用动能定理,有
Fsn-1=
解得sn-1=
本题难度:一般
4、选择题 两根磁铁放在两辆小车上,小车能在水平面上自由移动,甲车与磁铁总质量为1kg,乙车与磁铁总质量为2kg,两根磁铁的S极相对,推动一下使两车相向而行,若某时刻甲的速度为3m/s,乙的速度为2m/s,可以看到,他们还没有碰上就分开了,则?(?)
A.甲车开始反向时,乙车速度减为0.5m/s,方向不变
B.乙车开始反向时,甲车速度减为0.5m/s,方向与原来方向相反
C.两车距离最近时,速率相等,方向相反
D.两车距离最近时,速度都为0.33m/s,方向都与乙车原来的速度方向一致
参考答案:ABC
本题解析:取水平向右方向为正方向.
乙车开始反向时速度为零,根据动量守恒定律得,m甲v甲-m乙v乙=m甲v甲′,代入解得v甲′=0.5m/s,方向与原来方向相同.当两车速度相同时,相距最近,设共同速度为v,则有m甲v甲-m乙v乙=(m甲+m乙)v,代入解得v="0.33" m/s,水平向右,与乙车原来的速度相反.
本题难度:一般
5、简答题 一个质量为M的雪橇静止在水平雪地上,一条质量为m的爱斯基摩狗站在该雪橇?上.狗向雪橇的正后方跳下,随后又追赶并向前跳上雪橇;其后狗又反复地跳下、追赶并跳上雪橇.狗与雪橇始终沿一条直线运动.若狗跳离雪橇时雪橇的速度为V,则此时狗相对于地面的速度为V+u(其中u为狗相对于雪橇的速度,V+u为代数和,若以雪橇运动的方向为正方向,则V为正值,u为负值).设狗总以速度v追赶和跳上雪橇,雪橇与雪地间的摩擦忽略不计.已知v的大小为5m/s,u的大小为4m/s,M=30kg,m=10kg.
(1)求狗第一次跳上雪橇后两者的共同速度的大小.
(2)求雪橇最终速度的大小和狗最多能跳上雪橇的次数.(供使用但不一定用到的对数值:lg?2=0.301,lg?3=0.477)
参考答案:(1)设雪橇运动的方向为正方向.狗第1次跳下雪橇后雪橇相对地面的速度为V1,则此时狗相对于地面的速度为(V+μ),
由于雪橇和地面之间的摩擦忽略不计,故狗和雪橇组成的系统水平向动量守恒,
根据动量守恒定律,有MV1+m(V1+u)=0…①
设狗第1次跳上雪橇时,雪橇与狗的共同速度为V1’
由于此时狗和雪橇组成的系统水平向动量仍然守恒,则有?MV1+mv=(M+m)V1’…②
联立①②两式可得?V′1=-Mmu+(M+m)mv(M+m)2…③
将u=-4?m/s,v=5?m/s,M=30?kg,m=10?kg代入③式可得V1’=2?m/s
(2)解法(一)
设雪橇运动的方向为正方向.狗第(n-1)次跳下雪橇后雪橇的速度为vn-1,则狗第(n-1)次跳上雪橇后的速度Vn-1’,
满足M?Vn-1+mv=(M+m)?Vn-1’…④
这样,狗n次跳下雪橇后,雪橇的速度为Vn满足
M?Vn+m(Vn+u)=(M+m)?Vn-1’…⑤
解得?Vn=(v-u)[1-(MM+m)n-1]-muM+m(MM+m)n-1
狗追不上雪橇的条件是?vn≥v
可化为?(MM+m)n-1≤(M+m)uMu-(M+m)v
最后可求得?n≥1+lg(Mu-(M+m)v(M+m)u)lg(M+mM)
代入数据,得n≥3.41
故狗最多能跳上雪橇3次,雪橇最终的速度大小为?v4=5.625?m/s
解法(二):
设雪橇运动的方向为正方向.狗第i次跳下雪橇后,雪橇的速度为Vi′狗的速度为Vi+u;狗第i次跳上雪橇后,雪橇和狗的共同速度为Vi′,由动量守恒定律可得
第一次跳下雪橇:MV1+m(V1+u)=0…④
V1=-muM+m=1m/s
第一次跳上雪橇:MV1+mv=(M+m)V1’…⑤
?V′1=-Mmu+(M+m)mv(M+m)2
第二次跳下雪橇:(M+m)V1’=MV2+m(V2+u)…⑥
V2=(M+m)V′1-muM+m=3m/s
第二次跳上雪橇:MV2+mv=(M+m)V2’…⑦
V′2=MV2+mvM+m
第三次跳下雪橇:(M+m)V2’=MV3+m(V3+u)…⑧
V3=(M+m)V′2-muM+m=4.5m/s
第三次跳上雪橇:(M+m)V3=MV3’+m(V3’+u)…⑨
V′3=(M+m)V3-muM+m
第四次跳下雪橇:(M+m)V3’=MV4+m(V4+u)…⑩
V4=(M+m)V′3-muM+m=5.625m/s
此时雪橇的速度已大于狗追赶的速度,狗将不可能追上雪橇.
因此,狗最多能跳上雪橇3次.雪橇最终的速度大小为5.625m/s.
本题解析:
本题难度:一般