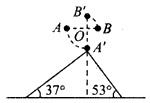
1、简答题  如图所示，一高度为h=0.2m的水平面在A点处与一倾角为θ=30°的斜面连接，一小球以v0=5m/s的速度在水平面上向右运动．求小球从A点运动到地面所需的时间（平面与斜面均光滑．g取10m/s2）．某同学对此题的解法为：小球沿斜面运动，则

2、实验题  在“研究平抛物体运动”的实验中，可以描绘平抛物体运动轨迹和求物体的平抛初速度。实验简要步骤如下：
A．让小球多次从___________位置上滚下，记下小球穿过卡片孔的一系列位置；
B．安装好器材，注意斜槽末端水平和平板竖直，记下斜槽末端O点和过O点的竖直线，检测斜槽末端水平的方法是___________。
C．测出曲线上某点的坐标x、y，用v0?=___________算出该小球的平抛初速度，实验需要对多个点求v0的值，然后求它们的平均值。
D．取下白纸，以O为原点，以竖直线为轴建立坐标系，用平滑曲线画平抛轨迹。
上述实验步骤的合理顺序是___________（只排列序号即可）。

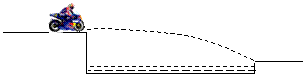
3、计算题  如图所示，一条小河两岸的高度差是h，河宽是高度差的4倍，一辆摩托车（可看作质点）以v0=20m/s的水平速度向河对岸飞出，恰好越过小河。若g=10m/s2，求：
（1）摩托车在空中的飞行时间；
（2）小河的宽度。

4、计算题  如图所示，一质点做平抛运动先后经过A、B两点，到达A点时速度方向与水平方向的夹角为30°，到达B点时速度方向与水平方向的夹角为60°。
（1）求质点在A、B位置的竖直分速度大小之比；
（2）设质点的位移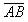与水平方向的夹角为θ，求tanθ的值。

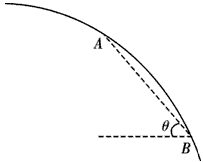
5、计算题  如图所示，轻直 杆长为2 m，两端各连着一个质量为1 kg的小球A、B，直杆绕着O点以ω=8 rad/s逆时针匀速转动，直杆的转动与直角斜面体在同一平面内。OA=1.5 m，A轨迹的最低点恰好与一个直角斜面体的顶点重合，斜面的底角为37°和53°，取g=10 m/s2。求：
（1）当A球通过最低点时，求B球对直杆的作用力；
（2）若当A球通过最低点时，两球脱离直杆（不影响两球瞬时速度，此后两球不受杆影响），此后B球恰好击中斜面底部，且两球跟接触面碰后小反弹，试求B球在空中飞行的时间；
（3）在（2）的情形下，求两球落点间的距离。