1、计算题  如图所示，质量为mA=2kg的木块A静止在光滑水平面上。一质量为mB= 1kg的木块B以某一初速度v0=5m/s沿水平方向向右运动，与A碰撞后都向右运动。木块A 与挡板碰撞后立即反弹（设木块A与挡板碰撞过程无机械能损失）。后来木块A与B发生二次碰撞，碰 后A、B同向运动，速度大小分别为0.9m/s、1.2m/s。求：

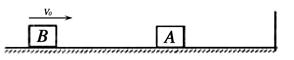
①第一次A、B碰撞后，木块A的速度；
②第二次碰撞过程中，A对B做的功。

参考答案：1）vA1＝2m/s? 2）0.22J

本题解析：
（2）（i）设A、B第一次碰撞后的速度大小分别为 vA1、vB1，去向右为正方向，则由动量守恒定律得mBv0＝mA vA1+mBvB1　?
A与挡板碰撞反弹，则第二次A、B碰撞前瞬间的速度大小分别为vA1、vB1，
设碰撞后的速度大小分别为vA2、vB2，取向左为正方向，
由动量守恒定律可得mAvA1-mBvB1＝mAvA2+mBvB2 ?
联立解得vA1＝2m/s，vB1＝1 m/s?
（ii）设第二次碰撞过程中，A对B做的功为W，根据动能定理W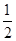＝mBvB22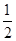－mBvB12=0.22J

本题难度：一般

2、计算题  如图所示，一带电为+q质量为m的小球，从距地面高h处以一定的初速水平抛出，在距抛出点水平距离为L处有根管口比小球略大的竖直细管，管的上口距地面h/2。为了使小球能无碰撞地通过管子（即以竖直速度进入管子），可在管子上方整个区域内加一水平向左的匀强电场，（重力加速度为g）求：
（1）小球的初速度；
（2）应加电场的场强；
（3）小球落地时的动能。

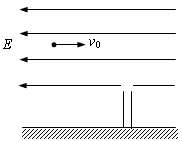
参考答案：解：（1）要使小球无碰撞地通过管口，则当它到达管口时，速度方向为竖直向下
竖直方向，自由落体运动，则运动时间为：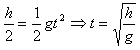
水平方向，粒子做匀减速运动，减速至0，位移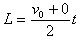
解得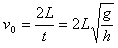
（2）水平方向，根据牛顿第二定律：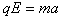
又由运动学公式：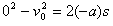
解得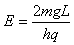，方向水平向右
（3）由动能定理：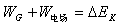
即：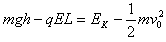
解得：EK=mgh

本题解析：

本题难度：困难

3、选择题  如图所示，在斜面倾角为θ的斜面底端，垂直斜面有一固定挡板。现有一质量为m（可视为质点）的物块以速度v0从P点沿斜面下滑，已知物块与斜面间动摩擦因数为μ(μ<tanθ)，P点距离挡板距离为L,物块与挡板碰撞时无能量损失，不计空气阻力，则有关下列说法正确的是：

A．物块第一次与挡板碰撞时的动能为
B．第一次与挡板碰后沿斜面上滑的最大距离一定小于L
C．从开始到物块静止，物块重力势能的减少量为
D．物块在斜面上通过的总路程为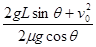

参考答案：CD

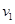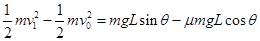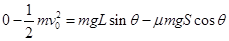本题解析：根据动能定理，在下落到挡板前设碰撞前速度为，利用动能定理则，所以A错。假设物体初速度为0，则第一次与挡板碰后沿斜面上滑的最大距离一定小于L，但由于有初速度，初速度对应的动能可能大于摩擦力消耗的能量，因此B错。从开始到物块静止，物块重力势能的减少量为，正确。利用动能定理，则块在斜面上通过的总路程为s，即，化简则
点评：本题考查了通过动能定理分析物体在外力作用下动能变化。

本题难度：一般

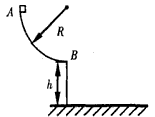
4、计算题  如图所示，半径R=2m的四分之一粗糙圆弧轨道AB置于竖直平面内，轨道的B端切线水平，且距水平地面高度为h=1.25m，现将一质量m=0.2kg的小滑块从A点由静止释放，滑块沿圆弧轨道运动至B点以v=5m/s的速度水平飞出（g取10m/s2）。求：
（1）小滑块沿圆弧轨道运动过程中所受摩擦力做的功；
（2）小滑块经过B点时对圆轨道的压力大小；
（3）小滑块着地时的速度大小和方向。

参考答案：解：（1）滑块在圆弧轨道受重力、支持力和摩擦力作用，由动能定理
mgR－Wf=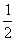mv2，Wf=1.5J
（2）FN－mg=m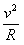，∴FN=4.5N
（3）小球离开圆弧后做平抛运动H=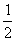gt2，∴t=0.5s
落地时竖直分速度vy=gt=5m/s
∴落地时速度大小v=5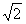m/s，方向与水平方向夹角为45°

本题解析：

本题难度：困难

5、选择题  如图所示，电梯质量为M，它的水平地板上放置一质量为m的物体，电梯在钢索的拉力作用下由静止开始竖直向上加速运动．当上升高度为H时，电梯的速度达到v，则在这段过程中，下列说法中正确的是（　　）
A．电梯地板对物体的支持力所做的功等于