1、简答题  两块质量都是m的木块A和B在光滑水平面上均以速度

参考答案：（1）在子弹打入木块A的瞬间，由于相互作用时间极短，
弹簧来不及发生形变，A、B都不受弹力的作用，故vB=12v0；
由于此时A不受弹力，木块A和子弹构成的系统在这极短过程中不受外力作用，系统动量守恒，
以子弹与A组成的系统为研究对象，以子弹的初速度方向为正方向，：
由动量守恒定律得：14mv0-m?v02=（14m+m）vA，解得：vA=-15v0，负号表示方向向左；
（2）由于木块A、木块B运动方向相同且vA＜vB，故弹簧开始被压缩，
分别给A、B木块施以弹力，使得木块A加速、B变减速运动，弹簧不断被压缩，
弹性势能增大，直到二者速度相等时弹簧弹性势能最大，
在弹簧压缩过程木块A（包括子弹）、B与弹簧构成的系统动量守恒，机械能守恒．
设弹簧压缩量最大时共同速度为v，弹簧的最大弹性势能为Epm，
以A、B与弹簧组成的系统为研究对象，以向左为正方向，
由动量守恒定律得：54mvA+mvB=（54m+m）v，
12?54mvA2+12mvB2=12（54m+m）v2+Epm，
解得：v=13v0，Epm=140mv02；
答：（1）在子弹击中木块后的瞬间木块A、B的速度分别为15v0、12v0；
（2）在子弹击中木块后的运动过程中弹簧的最大弹性势能为140mv02．

本题解析：

本题难度：一般

2、计算题  (4分)如图所示，质量分别为m1和m2的两个小球在光滑的水平面上分别以速度v1、v2同向运动并发生对心碰撞，碰撞后m2被右侧墙壁原速率弹回，又与m1相碰，碰后两球都静止，求：两球第一次碰撞后m1的速度。

参考答案：v′1＝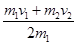

本题解析：以水平向右方向为正方向，第一次碰撞后瞬间，小球m1和m2的速度分别为v′1和v′2，整个碰撞过程两球系统的动量守恒，有：m1v1＋m2v2＝m1v′1＋m2v′2，m1v′1－m2v′2＝0，联立以上两式解得第一次碰撞后m1的速度为：v′1＝。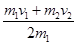

本题难度：一般

3、简答题  如图所示,在光滑水平面上,依次有质量为m，2m，3m……10m的10个小球，排列成一直线，彼此间有一定的距离，开始时后面的九个小球是静止的，第一个小球以初速度V0向着第二个小球碰去，结果它们先后全部粘合到一起向前运动．出于连续的碰撞，求系统损失的机械能为多少?

参考答案：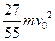

本题解析：
以系统为研究对象．
运用动量守恒，求一起向前运动的速度V

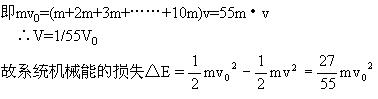
本题难度：简单

4、选择题  在光滑水平面上，两球沿球心连线相向而行，已知其动量大小相同并发生碰撞，下列现象可能的是
A．若两球动能不同，碰后以某一相等的速率相互分开
B．若两球动能相同，碰后以某一相等的速率相互分开
C．若两球动能不同，碰后一个球静止一个球运动
D．若两球动能相同，碰后两球都静止不动