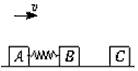
1、计算题  用轻弹簧相连的质量均为2 kg的A、B两物块都以v＝6 m／s的速度在光滑的水平地面上运动，弹簧处于原长，质量4 kg的物块C静止在前方，如图所示，B与C碰撞后二者两者立即粘在一起运动。求：在以后的运动中：?
（1）当弹簧的弹性势能最大时，物体A的速度多大？
（2）弹性势能的最大值是多大？?

参考答案：解：（1）当A、B、C三者的速度相等时弹簧的弹性势能最大
由于A、B、C三者组成的系统动量守恒，(mA+mB)v＝(mA+mB+mC)vA′ ?
解得vA′=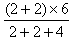 m/s=3 m/s ?
（2）B、C碰撞时B、C组成的系统动量守恒，设碰后瞬间B、C两者速度为v′，则?
mBv=(mB+mC)v′
v′=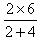=2 m/s?
设物A速度为vA′时弹簧的弹性势能最大为Ep
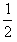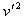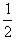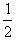根据能量守恒Ep=(mB+mC)+mAv2－(mA+mB+mC)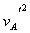=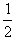×(2+4)×22+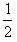×2×62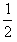－×(2+2+4)×32=12 J

本题解析：

本题难度：困难

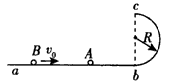
2、计算题  如图所示，abc是光滑的轨道，其中ab是水平的，bc是位于竖直平面内与ab相切的半圆，半径R=0.40 m。质量m=0.30 kg的小球A静止在水平轨道上，另一质量M=0.50 kg的小球B以v0=4 m/s的初速度与小球A发生碰撞。已知碰后小球A经过半圆的最高点c后落到轨道上距b点为L=1.2 m处，重力加速度g=10 m/s2。求：
(1)当A球经过半圆的最高点c时的速度大小；
(2)当A球经过半圆的最低点b时它对轨道的作用力；
(3)判断A，B碰撞是否是完全弹性碰撞。

参考答案：解：(1)设碰后小球A在半圆的最高点c时速度为vA"，球A随后离开c点做平抛运动，有
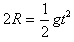，L=vA"t
解得vA"=3 m/s
(2)设碰后小球A在半圆的最低点b时速度为vA，小球A从b点到c点由机械能守恒定律得

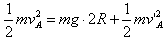
解得vA=5 m/s
在b点时，对A由牛顿运动定律可得：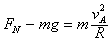
联立解得FN=21.75 N
根据牛顿第三定律，球对轨道的作用力FN"大小为21.75 N，方向竖直向下
(3)对碰撞过程，由动量守恒定律得Mv0=MvB+mvA
解得vB=1 m/s
由功能关系得，碰撞中产生的内能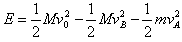
解得E=0
所以，球A，B的碰撞为完全弹性碰撞

本题解析：

本题难度：困难

3、计算题  （选修3-5选做题）
如图所示，质量为m2=10kg的滑块静止于光滑水平面上，一小球m1=5kg向右以v=5m/s的速度与滑块相碰，碰后滑块的速度为6m/s。求碰后小球的速度。

参考答案：解：?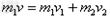

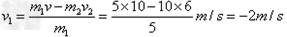
负号表示碰后小球的速度方向向左

本题解析：

本题难度：一般

4、简答题  如图1-3所示,质量为m的木块可视为质点，置于质量也为m的木盒内，木盒底面水平，长l="0.8" m,木块与木盒间的动摩擦因数μ=0.5,木盒放在光滑的地面上，木块A以v0="5" m/s的初速度从木盒左边开始沿木盒底面向右运动，木盒原静止.当木块与木盒发生碰撞时无机械能损失，且不计碰撞时间，取g="10" m/s2.问：
小题1:木块与木盒无相对运动时，木块停在木盒右边多远的地方？
小题2:在上述过程中，木盒与木块的运动位移大小分别为多少？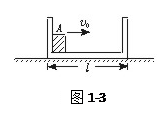

参考答案：
小题1:0.45 m
小题2:s盒="1.075" m?s块="1.425" m

本题解析：

小题1:木块相对木盒运动及与木盒碰撞的过程中，木块与木盒组成的系统动量守恒，最终两者获得相同的速度，设共同的速度为v,木块通过的相对路程为s,则有：
mv0=2mv?①
μmgs=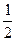mv02-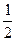·2mv2②
由①②解得s="1.25" m
设最终木块距木盒右边为d,由几何关系可得：
d=s-l="0.45" m
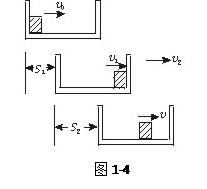
小题2:从木块开始运动到相对木盒静止的过程中，木盒的运动分三个阶段：第一阶段，木盒向右做初速度为零的匀加速运动；第二阶段，木块与木盒发生弹性碰撞，因两者质量相等，所以交换速度；第三阶段，木盒做匀减速运动，木盒的总位移等于一、三阶段的位移之和.为了求出木盒运动的位移，我们画出状态示意图，如图1-4所示.
设第一阶段结束时，木块与木盒的速度分别为v1、v2,则：
mv0=mv1+mv2?③
μmgL=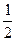mv02-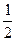m（v12+v22）?④
因在第二阶段中，木块与木盒转换速度，故第三阶段开始时木盒的速度应为v1,选木盒为研究对象
对第一阶段：μmgs1=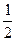mv22?⑤
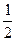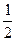对第三阶段：μmgs2=mv12-mv2?⑥
从示意图得s盒=s1+s2?⑦
s块=s盒+L-d?⑧
解得s盒="1.075" m?s块="1.425" m

本题难度：一般

5、简答题  质子的质量是1.67×10-27 kg，速度为1.0×107 m/s，跟一个静止的氦核碰撞后，质子以6.0×106 m/s的速度被反弹回来，氦核则以4.0×106 m/s的速度运动，氦核的质量为多少？

参考答案：6.68×10-27kg

本题解析：这是一个碰撞问题，它遵守动量守恒定律，这里只须弄清系统的初末状态即可.
以质子和氦核为一个系统.设质子质量为m1，作用前的速度为v1，作用后的速度为v1′，氦核的质量为m2，作用后的速度为v2′,以质子的初速度方向为正，由动量守恒定律：
m1v1+0=m1v1′+m2v2′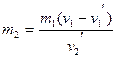　
代入数据得：

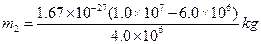
=6.68×10-27kg.

本题难度：简单