1、计算题  如图所示，小球Q在竖直平面内做匀速圆周运动，半径为r，当球Q运动到与O在同一水平线上时，有另一小球P在距圆周最高点为h处开始自由下落．要使两球在圆周最高点处相碰，Q球的角速度ω应满足什么条件？

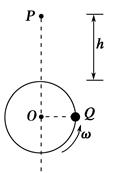
参考答案：Q球的角速度ω应满足ω＝π(4n＋1) 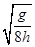(n＝0，1，2，…)

本题解析：小球Q在竖直平面内做匀速圆周运动具有周期性的特点，要求小球P在距圆周最高点为h处开始自由下落至在圆周最高点处相碰，则在小球P下落时间内小球Q转过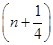圈，即小球P下落时间是小球Q匀速圆周运动周期的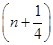倍．由此代入列方程即可求解．
自由落体的位移公式h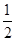＝gt2，可求得小球P自由下落运动至圆周最高点的时间为t1＝.
设小球Q做匀速圆周运动的周期为T，则有T＝，
由题意知，球Q由图示位置运动至圆周最高点所用时间为t2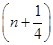＝T，式中n＝0，1，2，…
要使两球在圆周最高点相碰，需使t1＝t2.
以上四式联立，解得球Q做匀速圆周运动的角速度为ω＝π(4n＋1)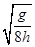式中n＝0，1，2…
即要使两球在圆周最高点处相碰，Q球的角速度ω应满足
ω＝π(4n＋1) 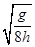(n＝0，1，2，…)．

本题难度：一般

2、计算题  如图所示，在质量为M的电动机上，装有质量为m的偏心轮，（偏心轮的重心距转轴r，偏心轮等效为用一长为r的细杆固定质量为m（轮的质量）的质点，绕转轴转动。）轮匀速转动，当轮重心在转轴正上方时，电动机对地面的压力刚好为零。
求：（1）当轮重心在转轴正上方时，细杆的作用力多大？
（2）轮转动的角速度ω多大?
（3）当轮重心在转轴正下方时，细杆的作用力多大？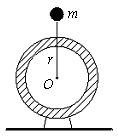

参考答案：（1）F=Mg（2）（3）（M＋2m）g

本题解析：（1）轮的重心在正上方时，电动机对地面的压力刚好为零，则此时偏心轮对电动机向上的作用力大小等于电动机的重力。即F=Mg? 2分?①
（2）根据牛顿第三定律，此时轴对偏心轮的作用力向下，大小为F=Mg，其向心力为
F＋mg=mω2r? 3分?②
由①②得偏心轮重心到转轴的距离为：? 2分③
（3）当偏心轮的重心转到最低点时，电动机对地面的压力最大.对偏心轮有
F′－mg=mω2r?3分?④
由③、④、⑤解得F′=（M＋2m）g?2分
电动机对地面的压力刚好为零，说明杆对电动机的拉力等于电动机的重力，再以m为研究对象，拉力和重力的合力提供向心力，列式求解

本题难度：一般

3、选择题  (2011年金华十校第一次联考)如图是自行车传动结构的示意图，其中Ⅰ是半径为r1的大齿轮，Ⅱ是半径为r2的小齿轮，Ⅲ是半径为r3的后轮，假设脚踏板的转速为n r/s，则自行车前进的速度为(　　)

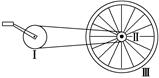
A．　　　　　　　　
B．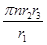
C．
D．

参考答案：选C.

本题解析：前进速度即为Ⅲ轮的线速度，由同一个轮上的角速度相等，同一条线上的线速度相等可得：ω1r1＝ω2r2，ω3＝ω2，再有ω1＝2πn，v＝ω3r3，所以v＝.

本题难度：一般

4、填空题  在一根轻质绳的一端拴一质量为1kg的小球，绳的另一端固定在光滑水平面上的O点，小球绕O点做匀速圆周运动的速率为2m/s，轻绳受到的拉力为8N，绳的长度为_________m。

参考答案：0.5

本题解析：由。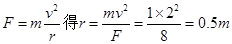

本题难度：简单

5、选择题  一小球质量为m，用长为L的悬绳（不可伸长，质量不计）固定于O点，在O点正下方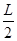处钉有一颗钉子，如图所示，将悬线沿水平方向拉直无初速度释放后，当悬线碰到钉子后的瞬间：

A．小球的线速度没有变化
B．小球的角速度没有变化
C．小球的向心加速度突然增大到原来的2倍
D．悬线对小球的拉力突然增大到原来的2倍

参考答案：AC

本题解析：
分析：小球在下摆过程中，受到线的拉力与小球的重力，由于拉力始终与速度方向相垂直，所以它对小球不做功，只有重力在做功．当碰到钉子瞬间，速度大小不变，而摆长变化，从而导致向心加速度变化，拉力变化．
解答：解：A、当碰到钉子瞬间，小球到达最低点时线速度没有变化，故A正确．
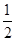B、根据圆周运动知识得：ω=，而半径变为原来的，线速度没有变化，所以小球的角速度突然增大到原来的2倍，故B正确．
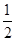C、根据圆周运动知识得：a=，而半径变为原来的，线速度没有变化，所以向心加速度突然增大到原来的2倍，故C正确；
D、小球摆下后由机械能守恒可知，mgL=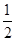mv2，
因小球下降的高度相同，故小球到达最低点时的速度相同，v=
在最低点根据牛顿第二定律得：F-mg=ma=m，
原来：r=L，F=mg+m=3mg
而现在半径变为原来的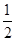，线速度没有变化．
所以F′=mg+m=5mg
悬线对小球的拉力突然增大到原来的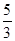倍，故D错误
故选AC．
点评：本题中要注意细绳碰到钉子前后转动半径的变化，再由向心力公式分析绳子上的拉力变化．小球摆到最低点虽与钉子相碰，但没有能量的损失．

本题难度：简单