1、计算题 如图所示,质量为的密度计,上部粗细均匀,横截面积为,漂浮在密度为的液体中。现将密度计轻轻按下一段后放手,密度计上、下起伏。若不计液体的阻力,试证明密度计做的是简谐振动。
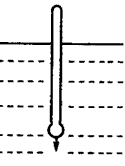
参考答案:解:简谐振动的重要特征是回复力大小与位移大小成正比,与位移方向相反。
取向下为正方向,液面为平衡位置。
密度计静止时,受重力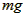 和浮力
和浮力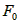 ,且有
,且有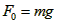 ;即
;即 ,
,
其中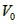 是密度计静止时浸没在液体中的体积。
是密度计静止时浸没在液体中的体积。
当密度计向下位移为x时,所受浮力为: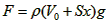 ,回复力为:
,回复力为: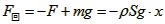 ;
;
当密度计向上位移为-x时,所受浮力为: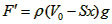 ,
,
回复力为: ;
;
令 ,则恒有:
,则恒有: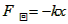 ,密度计所受回复力与位移成正比,方向相反,故密度计的振动是简谐振动。
,密度计所受回复力与位移成正比,方向相反,故密度计的振动是简谐振动。
本题解析:
本题难度:一般
2、选择题 一物体从斜面顶端由静止开始匀加速下滑直到底端,最初3秒内的位移x1=4.5m,最后3秒内的位移x2=10.5m.则斜面长度及物体在斜面上运动的时间分别是
A.15m,6s
B.24.5m,7s
C.15m,5s
D.12.5m,5s
参考答案:D
本题解析:分析:根据最初3s内的位移求出物体运动的加速度,最后3s内的平均速度等于中间时刻的瞬时速度,通过瞬时速度和加速度,求出运动到最后3s中间时刻的时间,从而知道总时间,根据位移时间公式求出斜面的长度.
解答:根据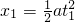 得,a=
得,a=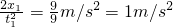 .
.
最后3s内的中间时刻瞬时速度
根据v′=at′知,t′=3.5s.
所以运动的总时间t=3.5+1.5s=5s.
x=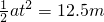 .故D正确,A、B、C错误.
.故D正确,A、B、C错误.
故选D.
点评:解决本题的关键掌握匀变速直线运动的规律,灵活运用运动学公式进行求解.
本题难度:一般
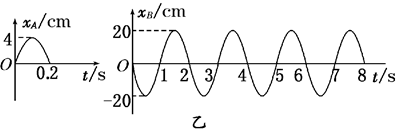
3、计算题 (10分)如图甲所示,在某介质中波源A、B相距d=20 m,t=0时两者开始上下振动,A只振动了半个周期,B连续振动,所形成的波的传播速度都为v=1.0 m/s,开始阶段两波源的振动图象如图乙所示.
(1)求距A点1米处的质点,在t=0到t=22 s内所经过的路程?
(2)求在t=0到t=16 s内从A发出的半个波前进过程中所遇到的波峰个数?
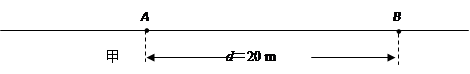
参考答案:(1)128cm?(2)6个
本题解析:(1) 距A点1米处的质点在先经过左边的A波路程为
s1=2×4cm=8cm(2分)
B波22秒传播的距离为:x=vt=22m;B波的波长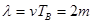 (1分)
(1分)
B波已经传播过距A点1米处的质点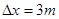 ;经过此点1.5个波长,
;经过此点1.5个波长,
故此点又振动的路程为s2=6×20cm=120cm;(1分)
距A点1米处的质点,在t=0到t=22 s内所经过的路程:
s=s1+s2=128cm?(1分)
(2)16 s内两列波相对运动的长度为:Δ l=lA+lB-d=2vt-d=12 m,(2分)
A波宽度为a=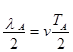 =0.2 m.;B波波长为λB=vTB=2 m?(2分)
=0.2 m.;B波波长为λB=vTB=2 m?(2分)
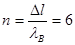 ;可知A波经过了6个波峰.(1分)
;可知A波经过了6个波峰.(1分)
本题难度:一般
4、填空题 图中实线是一列简谐波在某一时刻的波形图线,虚线是0.2s后它的波形图线。这列波可能的传播速度是_______。
参考答案:(20n+5)m/s和(20m+15)m/s,(n=0,1,2,…)
本题解析:
【错解分析】错解:从图上可以看出波长λ=4m,而从两次的波形图可知:
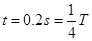 ,
,
所以T=0.8s
由波速公式: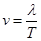 ,
,
代入数据v=5m/s.
(1)在没有分析出此波的传播方向前,就认定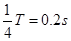 ,是不全面的。实际上,只有当波向右(沿x正方向)传播时,上述关系才成立。
,是不全面的。实际上,只有当波向右(沿x正方向)传播时,上述关系才成立。
(2)没有考虑到波的传播过程的周期性。也就是说,不仅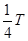 后的波形如虚线所示。
后的波形如虚线所示。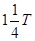 ,
,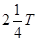 ……后的波形均与
……后的波形均与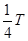 后的波形相同。
后的波形相同。
【正解】从图上可以看出λ=4m。
当波沿x正方向传播时,两次波形之间间隔的时间为:
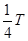 ,
,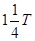 ,
,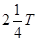 ……
……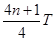
而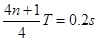 ?
?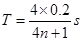
由波速公式: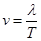 ,代入数据
,代入数据
解得: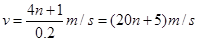 (n=0,1,2……)
(n=0,1,2……)
当波沿x正方向传播时,两次波形之间间隔的时间为:
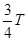 ,
,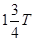 ,
,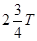 ……
……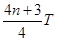
而 ?
?
由波速公式: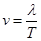 ,代入数据
,代入数据
解得: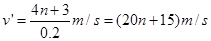 (n=0,1,2……)
(n=0,1,2……)
此题的答案为:(20n+5)m/s和(20m+15)m/s,(n=0,1,2,…)
【点评】对于这种已知条件较为含糊的波的问题,要从波的传播方向、时间和空间的周期性等方面进行全面周到的分析,这也是解决机械波问题时,初学者经常忽略的问题。
本题难度:一般
5、简答题 弹簧振子以O点为平衡位置在B、C两点之间做简谐运动.B、C相距20cm.某时刻振子处于B点.经过0.5s,振子首次到达C点.求:
(1)振动的周期;
(2)振子在5s内通过的路程及偏离平衡位置的位移大小.
参考答案:(1)振子从B到C所用时间t=0.5s,为周期T的一半,所以T=1.0s.
(2)设振幅为A,由题意BC=2A=20cm,所以A=10cm.
振子在1个周期内通过的路程为4A,故在t=5s=5T内通过的路程s=tT?4A=200cm.
5s内振子振动了5个周期,5s末振子仍处在B点,所以它偏离平衡位置的位移大小为x=10cm.
答:(1)振动的周期为1s;
(2)振子在5s内通过的路程是200cm,偏离平衡位置的位移大小为10cm.
本题解析:
本题难度:一般