1、简答题  倾角θ=37°的斜面体固定在水平地面上，一根轻绳跨过固定在斜面顶端的定滑轮，绳的一端与质量为ml=1kg的物块A连接，且绳与斜面平行；另一端与质量为m2=3kg的物块B连接．开始时，用手按住A，使B悬于距地面高H=0.6m处，而A静止于斜面底端．如图所示．现释放B，试求此后A在斜面上向上滑行的最大距离？（设斜面足够长，且所有接触面间的摩擦均忽略不计，sin37°=0.6，cos37°=0.8，g取10m/s2）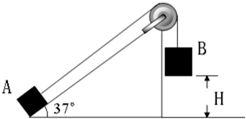

参考答案：设B落地时的速度为v，系统的机械能守恒：
?m2gH-m1gHsinθ=12（m1+m2）v2? ①
?B落地后，A以v为初速度沿斜面匀减速上升，设沿斜面又上升的距离为S，
由动能定理得：-m1gSsinθ=0-12mv2 ?②
物体m能沿斜面滑行的最大距离：L=h+S?③
由①②③代入数据得：L=1.2m
答：物体A能沿斜面滑行的最大距离是1.2m．

本题解析：

本题难度：一般

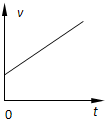
2、选择题  下图是某物体做直线运动的各种图象，其中v、a、F、Ek分别表示物体的速度、加速度、所受到的合外力、动能，则该物体一定不做匀变速直线运动的是（　　）
A．

B．

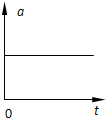
C．

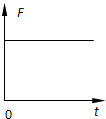
D．

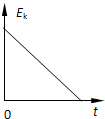
参考答案：D

本题解析：

本题难度：简单

3、简答题  已知某高速公路的最高限速为v="40" m/s.假设前方汽车突然停止，后面司机发现这一情况，经操纵刹车到汽车开始减速经历的时间（即反应时间）t="0.5" s.刹车时汽车的加速度大小为4 m/s2.求该高速公路上行驶的汽车的距离至少应为多大？

参考答案：220 m

本题解析：前方汽车突然停止，后面的汽车在司机反应时间内以原速率做匀速直线运动，然后做匀减速直线运动直到停止.
设在司机反应时间内后面的汽车的位移为s1，则有：s1="vt=20" m
设后面的汽车做减速运动到停止的位移为s2，由匀变速运动的规律可知：0-v2=-2as2
解得：s2=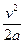="200" m
后面的汽车从司机发现前面的汽车停止到自己停下来所走的总的距离为：
s=s1＋s2="220" m
故高速公路上行驶的汽车的距离至少应为220 m.

本题难度：简单

4、简答题  甲车以10m/s的速度匀速行驶，当它经过一个路标时，乙车立即从路标处以加速度2m/s2由静止开始作匀加速直线运动追赶甲车，两车的运动方向相同，已知乙车的最大速度足够大．求：
（1）在乙车追上甲车之前，何时两车相距最远？两车距离的最大值是多少？
（2）乙车出发后经多长时间可追上甲车？此时它们离路标多远？

参考答案：（1）两车速度相等时，相距最远．
? t=v甲a=102s=5s
此时甲车的位移x1=v甲t=10×5m=50m
乙车的位移x2=12at2=12×2×25m=25m
△x=x1-x2=50-25m=25m
故经过5s两车相距最远，最大距离为25m．
（2）设经过t′时间乙车追上甲车．
vAt′=12at′2
10t′=12×2t′2，
解得，t′=10s
x=vAt′=100m
故经过10s乙车追上甲车，此时它们离路标100m．

本题解析：

本题难度：一般

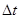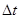5、计算题  一辆轿车违章超车，以30m/s的速度驶入左侧逆行车道时，猛然发现正前方80 m处一辆卡车正以20m/s的速度迎面驶来，两车司机同时刹车，刹车时加速度大小都是10 m/s2．两司机的反应时间（即司机从发现险情到实施刹车所经历的时间）都是，试问为何值，才能保证两车不相撞？

参考答案：0.3s

本题解析：两司机在反应时间内都做匀速直线运动，然后做匀减速直线运动，抓住两车的位移之和小于80m，求出△t最小值．
设轿车行驶的速度为v1，卡车行驶的速度为v2，则v1="108" km/h="30" m/s，v2="72" km/h="20" m/s，在反应时间△t内两车行驶的距离分别为s1、s2，则
s1=v1△t?①
s2=v2△t?②
轿车、卡车刹车所通过的距离分别为s3、s4
则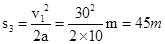?③
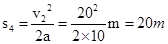?④
为保证两车不相撞，必须?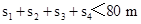?⑤
将①②③④代入⑤解得△t＜0.3 s
故△t＜0.3 s，才能保证两车不相撞
点评：解决本题的关键知道在反应时间内两车做匀速直线运动，刹车后做匀减速直线运动．两车的位移之和要小于80m．

本题难度：一般