1、选择题 从高为H的平台上同时水平抛出两个物体A和B,已知它们的质量mB=2mA,抛出时的速度vA=2vB,不计空气阻力,它们下落过程动量变化量的大小分别为ΔpA和ΔpB,则(? )
A.ΔpA=ΔpB
B.ΔpA=2ΔpB
C.ΔpB=4ΔpA
D.ΔpB=2ΔpA
参考答案:D
本题解析:平抛运动的时间为t=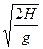 ?
?
由动量定理:Δp=F合·t=mg·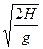 =m
=m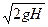 ∝m,所以ΔpB=2ΔpA.
∝m,所以ΔpB=2ΔpA.
本题难度:简单
2、简答题 如图18-1,劲度系数为k的轻质弹簧一端固定在墙上,另
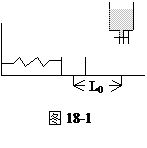
一端和质量为M的容器连接,容器放在光滑水平的地面上,
当容器位于O点时弹簧为自然长度,在O点正上方有一滴管,
容器每通过O点一次,就有质量为m的一个液滴落入 容器,
容器,
开始时弹簧压缩,然后撒去外力使容器围绕O点往复运动,?
求:
小题1:(1)容器中落入n个液滴到落入(n+1)个液滴的时间间?
隔;
小题2:(2)容器中落入n个液滴后,容器偏离O点的最大位移。
参考答案:
小题1:△t =π
小题2:Ln=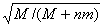 L0
L0
本题解析:本题中求容器内落入n个液滴后偏离O点的最大位移时,若从动量守恒和能量守恒的角度求解,将涉及弹簧弹性势能的定量计算,超出了中学大纲的要求,如果改用动量定理和动量守恒定律求解,则可转换成大纲要求的知识的试题。?
小题1:(1)弹簧振子在做简谐运动过程中,影响其振动周期的因素有振子的质量和恢复系数(对弹簧振子即为弹簧的劲度系数),本题中恢复系数始终不变,液滴的落入使振子的质量改变,导致其做简谐运动的周期发生变化。
容器中落入n个液滴后振子的质量为(M+nm),以n个液滴落入后到第(n+1)个液滴落入前,这段时间内系统做简谐运动的周期Tn=2π ,容器落入n个液滴到(n+1)个液滴的时间间隔△t=Tn /2,所以
,容器落入n个液滴到(n+1)个液滴的时间间隔△t=Tn /2,所以
△t =π
小题2:(2)将容器从初始位置释放后,振子运动的动量不断变化,动量变化的原因是水平方向上弹簧弹力的冲量引起的,将容器从静止释放至位置O的过程中,容器的动量从零增至p,因容器位于O点时弹簧为自然长度,液滴在O点处落入容器时,容器和落入的液滴系统在水平方向的合力为零, 根据动量守恒定律,液滴在O处的落入并不改变系统水平方向的动量,所以振子处从位置O到两侧相应的最大位移处,或从两侧相应在的最大位移处到位置O的各1/4周期内,虽然周期Tn和对应的最大位移Ln在不断变化,但动量变化的大小均为△p=p-0=p,根据动量定理可知识,各1/4周期内弹力的冲量大小均相等,即:
F0(t)·T0/4 = Fn(t)·Tn/4
其中T0是从开始释放到第一次到O点的周期,T0=2π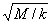 。Tn是n个液滴落入后到(n+1)个液滴落入容器前振子的周期,Tn=2π
。Tn是n个液滴落入后到(n+1)个液滴落入容器前振子的周期,Tn=2π 。而F0(t) 和Fn(t)分别为第一个1/4周期内和n个液滴落入后的1/4周期内弹力对时间的平均值,由于在各个1/4周期内振子均做简谐运动,因而弹力随时间均按正弦(或余弦)规律变化,随时间按正弦(或余弦)变化的量在1/4周期内对时间的平均值与最大值之间的关系,可用等效方法求出,矩形线圈在匀强磁场中匀速转动时,从中性而开始计地,产生的感应电动势为ε=εmsinωt= NbωSsinωt。ε按正弦规律变化,根据法拉第电磁感应定律ε=N
。而F0(t) 和Fn(t)分别为第一个1/4周期内和n个液滴落入后的1/4周期内弹力对时间的平均值,由于在各个1/4周期内振子均做简谐运动,因而弹力随时间均按正弦(或余弦)规律变化,随时间按正弦(或余弦)变化的量在1/4周期内对时间的平均值与最大值之间的关系,可用等效方法求出,矩形线圈在匀强磁场中匀速转动时,从中性而开始计地,产生的感应电动势为ε=εmsinωt= NbωSsinωt。ε按正弦规律变化,根据法拉第电磁感应定律ε=N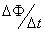 ,ε在1/4周期内对时间的平均值ε=2εm/π。这一结论对其它正弦(或余弦)变化的量对时间的平均值同样适用,则有
,ε在1/4周期内对时间的平均值ε=2εm/π。这一结论对其它正弦(或余弦)变化的量对时间的平均值同样适用,则有
F0(t)=2kL0/π,Fn(t)=2kLn/π
代入前式解得:Ln=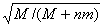 L0
L0
本题难度:简单
3、选择题 下列说法中正确的是( )
A.牛顿定律可以用物体动量的变化率来表示
B.一群处于n=3能级激发态的氢原子,自发跃迁时能发出3种不同频率的光
C.α粒子散射实验可以用来确定原子核电荷量和估算原子核半径
D.氢原子辐射出一个光子后能量减小,核外电子的运动加速度减小
参考答案:ABC
本题解析:
本题难度:一般
4、选择题 两辆小车A、B,其质量关系为mA>mB,车轮与水平地面间的动摩擦因数相等,现使它们以相同的动能沿水平地面滑行,则两车滑行距离sA、sB的大小关系是
A.sA=sB
B.sA>sB
C.sA<sB
D.条件不足,无法比较
参考答案:C
本题解析:
本题难度:一般
5、选择题 力F作用在质量为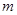 的物体上,在时间
的物体上,在时间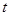 内物体速度由
内物体速度由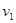 变为
变为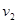 ,则力2F作用在质量为
,则力2F作用在质量为 的物体上,在时间
的物体上,在时间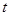 内物体动量的变化为?(?)
内物体动量的变化为?(?)
A.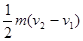
B.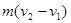
C.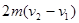
D.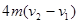
参考答案:C
本题解析: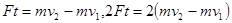 ,力的冲量与物体的质量无关
,力的冲量与物体的质量无关
本题难度:简单