1、计算题  如图所示，在光滑的桌面上叠放着一质量为mA=2.0kg的薄木板A和质量为mB=3 kg的金属块B，A的长度L=2.0m。B上有轻线绕过定滑轮与质量为mC=1.0 kg的物块C相连。B与A之间的滑动摩擦因数μ=0.10，最大静摩擦力可视为等于滑动摩擦力。忽略滑轮质量及与轴间的摩擦，起始时令各物体都处于静止状态，绳被拉直，B位于A的左端（如图），然后放手，求经过多长时间t后B从A的右端脱离。（设A的右端距滑轮足够远，取g=10m/s2）

参考答案：解：设aA表示A的加速度，aB表示B、C的加速度，sA和sB分别表示t时间A和B移动的距离，则由牛顿定律和匀加速运动的规律可得
mCg-μmBg=（mC+mB）aB
μmBg=mAaA
sB=aBt2
sA=aAt2
sB-sA=L
由以上各式，代入数值，可得t=4.0s

本题解析：

本题难度：一般

2、填空题  1999年11月20日，我国发射了“神舟号”载入飞船，次日载入舱着陆，实验获得成功．载人舱在将要着陆之前，由于空气阻力作用有一段匀速下落过程，若空气阻力与速度的平方成正比，比例系数k，载人舱的质量为m，则此过程中载人舱的速度应为______．

参考答案：
由于空气阻力作用载人舱匀速下落，则
mg=F
又空气阻力为：F=kv2
联立两式解得：
v=

本题解析：

本题难度：一般

3、简答题  如图所示，固定在水平地面上的桌子，高度h=0.8m，桌面上放着一块木板，木板的质量M=1.0kg，长度L=1.5m，厚度可以忽略不计，木板左右两端与桌面的两端对齐．质量m=1.0kg的小物块放在距木板左端d=0.5m处（小物块可视为质点）．木板与桌面间的摩擦忽略不计．现对木板施加一个F=12N水平向右的恒力，木板与物块发生相对滑动，经过一段时间物块离开木板，在桌面上运动一段距离后，从桌面的右端滑出，最后落在地面上．取g=10m/s2．求：
（1）物块在木板上运动的时间；
（2）物块落地点与桌面右端的水平距离．

参考答案：如图分别对M和m进行受力分析和运动分析有：

（1）小物块在木板上滑动时，根据牛顿第二定律
f1=μ1mg=ma1
a1=μ1g=4.0m/s2，方向向右
木板在水平方向上的受力情况如答图1所示，根据牛顿第二定律
F-μ1mg=Ma2
a2=F-μ1mgM=8.0m/s2
设经过时间t1，物块与木板分离，
物块的位移x1=12a1t12
木板的位移x2=12a2t12
由答图2可知x2-x1=d
解得t1=0.5s
（2）物块与木板分离时，物块的速度
υ1=a1t1=2.0m/s
物块在桌面上做匀减速直线运动，设物块运动到
桌面右端时的速度为υ2，根据牛顿第二定律
f2=μ2mg=ma3
a3=μ2g=3.0m/s2，方向向左
v22-v12=2(-a3)(L-d-x1)
x1=0.5m
解得υ2=1m/s
物块做平抛运动，设经过时间t2落地
h=12gt22?t2=

本题解析：

本题难度：简单

4、简答题  如图所示，一小物块从斜面上的A点由静止开始滑下，最后停在水平面上的C点．已知斜面的倾角θ=37°，小物块的质量m=0.10kg，小物块与斜面和水平间的动摩擦因数均为μ=0.25，A点到斜面底端B点的距离L=0.50m，设斜面与水平面连接，小物块滑过斜面与水平面连接处时无能量损失．求：
（1）小物块在斜面上运动时的加速度；
（2）BC间的距离为多大？（g=10m/s2）

参考答案：（1）小物块受到斜面的摩擦力：f1=μN1=μmgcosθ
在平行斜面方向由牛顿第二定律有：mg sinθ-f1=ma
解得：a=gsinθ-μgcosθ=4.0m/s2
（2）小物块由A运动到B，根据运动学公式有：v2B-v2A=2aL
解得：vB=

本题解析：

本题难度：一般

5、计算题  如图所示，一辆汽车以V0=15m/s的速率通过一座拱桥的桥顶时，汽车对桥面的压力等于车重的一半。取g =10m/s2,求：

（1）这座拱桥的半径R；
（2）若要使汽车过桥顶时对桥面恰无压力，则汽车过桥顶时的速度V的大小．

参考答案：（1）45m?（2）

本题解析：解决本题的关键是知道物体做圆周运动，径向的合力提供物体做圆周运动的向心力．
（1）设小车质量为m，桥面对小车支持力为，因汽车对桥面的压力等于车重的一半，由牛顿第三定律可知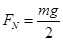
以汽车为研究对象，分析受力可知，过桥顶时由重力和桥顶的支持力的合力提供汽车的向心力，根据牛顿第二定律有：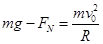
联立以上两式解得：
（2）汽车过桥顶时对桥面恰无压力，由牛顿第三定律得知，汽车过桥顶时不受支持力，故只受重力，则重力提供汽车所需的向心力，根据牛顿第二定律有：
所以

本题难度：一般