1、简答题
(1)在B释放后经过多少时间连接A、B的细绳将被拉直?
(2)在细绳将要拉直时A和B的速分别度为多大?
参考答案:(1)0.2s ?(2)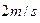
本题解析:
(1)设,B释放后t秒细绳被拉直,
由运动学公式得:
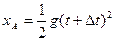 ? 1分
? 1分
 ? 1分
? 1分
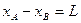 ? 1分
? 1分
由以上三式得:? t="0.2s?" 1分
(2)
 ? 2分
? 2分
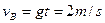 ? 2分
? 2分
本题难度:简单
2、简答题 如图所示,竖直放置的两块足够大的带电平行板间形成一个方向水平向右的匀强电场区域,场强E=3×104?N/C.在两板间用绝缘细线悬挂一个质量m=5×10-3?kg的带电小球,静止时小球偏离竖直方向的夹角θ=60°(g取10m/s2).试求:
(1)小球的电性和电荷量;
(2)悬线的拉力;
(3)若小球静止时离右板d=5
×10-2?m,剪断悬线后,小球经多少时间碰到右极板.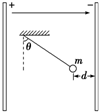
参考答案:
本题解析:
本题难度:一般
3、计算题 (14分)鸡蛋从高处落到地面而不被摔坏,撞击地面的速度最大不能超过1.0m/s。课外活动小组设计了如图所示的保护装置,用A、B两块较粗糙的夹板夹住鸡蛋,现将该装置从距地面某一高处自由下落,装置碰地后速度立即为0,且保持竖直无反弹,此后鸡蛋在A、B夹板间减速下降的加速度为4.5g。某次实验中保护装置从离地面H=5m的高度处静止释放。(g =10m/s2)

(1)如果没有保护,鸡蛋自由下落而不被摔坏时释放的最大高度h;
(2)实验中为保证鸡蛋安全,鸡蛋放的位置离装置下端的最小距离s;
(3)在(2)情况下鸡蛋运动的总时间t。
参考答案:(1) (2)
(2) (3)
(3)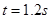
本题解析:(1)鸡蛋做自由落体运动,由匀变速直线运动公式可得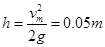
(2)设鸡蛋和保护装置在自由下落过程中着地时的速度为v,则有:
 ,解得
,解得
鸡蛋仔保护装置中减速下落时有: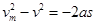 ,故
,故
(3)鸡蛋下落时间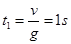
鸡蛋减速下落时间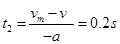
鸡蛋运动的总时间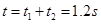
本题难度:一般
4、选择题 用比值定义物理量是物理学中一种常用方法,下面有四个物理量:①电场强度E=F/q②电势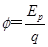 ③电容
③电容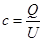 ④电场强度
④电场强度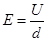 ,其中不属于比值法定义的是(?)
,其中不属于比值法定义的是(?)
A.①
B.②
C.③
D.④
参考答案:D
本题解析:比值定义物理量的方法就是指在定义某一个物理量的时候采取比值的形式定义的,即将某一物理量作为分子,另一物理量作为分母,把得到的比值定义为新的物理量的一种方法。电场强度的定义是放入电场中某点的电荷所收的电场力F跟它的电荷量q的比值;电势的定义是某点电荷的电势能跟它所带的电荷量之比;电容是指任一极板上的带电量与两极板间的电压的比值是一个常数。比值式中等号左边的物理量不随右边的物理量改变而改变。而电场强度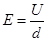 是一条推导出来的公式。故本题选D
是一条推导出来的公式。故本题选D
本题难度:简单
5、简答题 有一竖直放置、两端封闭的长玻璃管,管内为真空,管内有一小球自某处自由下落(初速度为零),落到玻璃管底部时与底部发生弹性碰撞.以后小球将在玻璃管内不停地上下跳动.现用支架固定一照相机,用以拍摄小球在空间的位置.每隔一相等的确定的时间间隔T拍摄一张照片,照相机的曝光时间极短,可忽略不计.从所拍到的照片发现,每张照片上小球都处于同一位置.求小球开始下落处离玻璃管底部距离(用H表示)的可能值以及与各H值相应的照片中小球位置离玻璃管底部距离的可能值.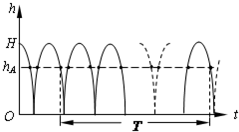
参考答案:小球沿竖直线上下运动时,其离开玻璃管底部的距离h随时间t变化的关系如图所示.设照片拍摄到的小球位置用A表示,A离玻璃管底部的距离为hA,小球开始下落处到玻璃管底部的距离为H.小球可以在下落的过程中经过A点,也可在上升的过程中经过A点.现以τ表示小球从最高点(即开始下落处)落到玻璃管底部所需的时间(也就是从玻璃管底部反跳后上升到最高点所需的时间),τ1表示小球从最高点下落至A点所需的时间(也就是从A点上升至最高点所需的时间),τ2表示小球从A点下落至玻璃管底部所需的时间(也就是从玻璃管底部反跳后上升至A点所需的时间).显然,τ1+τ2=τ.根据题意,在时间间隔T 的起始时刻和终了时刻小球都在A点.用n表示时间间隔 T 内(包括起始时刻和终了时刻)小球位于A点的次数(n≥2).下面分两种情况进行讨论:
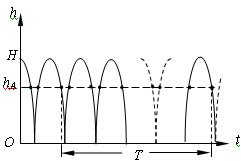
1.A点不正好在最高点或最低点.
当n为奇数时有
T=(n-1)τ1+(n-1)τ2=(n-1)τ? n=3,5,7,…(1)
在(1)式中,根据题意τ1可取0<τ1<τ中的任意值,而
τ2=τ-τ1 (2)
当n为偶数时有
T=nτ2+(n-2)τ1=nτ1+(n-2)τ2? n=2,4,6,…(3)
由(3)式得τ1=τ2 (4)
由(1)、(3)、(4)式知,不论n是奇数还是偶数,都有
T=(n-1)τ? n=2,3,4,…(5)
因此可求得,开始下落处到玻璃管底部的距离的可能值为
Hn=12gτ2=12g(Tn-1)2? n=2,3,4,…(6)
若用Hn表示与n对应的H值,则与Hn相应的A点到玻璃管底部的距离
hA=Hn-12gτ2 ?n=2,3,4,…(7)
当n为奇数时,τ1可取0<τ1<τ中的任意值,故有
0<hA<Hn[Hn=12g(Tn-1)2]n=3,5,7,?(8)
可见与Hn相应的hA的可能值为0与Hn之间的任意值.
当n为偶数时,τ1=12τ,由(6)式、(7)式求得Hn的可能值
hA=34Hn[Hn=12g(Tn-1)2]n=2,4,6,?(9)
2.若A点正好在最高点或最低点.
无论n是奇数还是偶数都有
T=2(n-1)τ? ?n=2,3,4,?(10)
Hn=12gτ2=12g[T2(n-1)]2? ?n=2,3,4,?(11)
hA=Hn? {Hn=12g[T2(n-1)]2} n=2,3,4,?(12)
或 hA=0 (13)
本题解析:
本题难度:一般