1、计算题  图中MN表示真空室中垂直于纸面的平板，它的一侧有匀强磁场，磁场方向垂直于纸面向里，磁感应强度大小为B。一带正电粒子从平板上狭缝O处以与平板成θ的初速度v射入磁场区域如图，最后到达平板上的P点。已知B、v以及P到O的距离l，不计重力，求此粒子的电荷量q与质量m之比。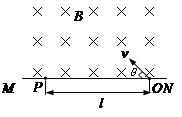

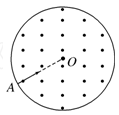
2、计算题  半径为R的绝缘圆筒中有沿轴线方向的匀强磁场，磁感应强度为B，如图所示．一质量为m、带电荷量为q的正粒子(不计重力)以速度v从筒壁的A孔沿半径方向进入筒内，设粒子和筒壁的碰撞无电荷量和能量的损失，那么要使粒子与筒壁连续碰撞，绕筒壁一周后恰好又从A孔射出，问：?
(1)磁感应强度B的大小必须满足什么条件？
(2)粒子在筒中运动的时间为多少？

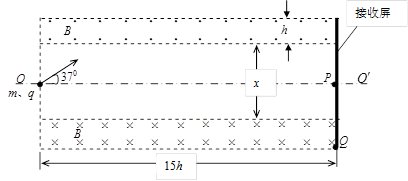
3、计算题  利用如图所示装置可调控带电粒子的运动，通过改变左端粒子入射速度的大小，可以控制粒子到达右端接收屏上的位置，装置的上下两个相同的矩形区域内存在匀强磁场，磁感应强度大小均为B、方向与纸面垂直且相反，磁场区域的宽度均为h，磁场区域长均为15h，P、Q为接收屏上的二点，P位于轴线上，Q位于下方磁场的下边界上。在纸面内，质量为m、电荷量为＋q的粒子以某一速度从装置左端的中点射入，方向与轴线成370角，经过上方的磁场区域一次，恰好到达Q点。不计粒子的重力 (sin370=0.6、cos370=0.8)。问：

（1）上下两磁场间距x为多少？
（2）仅改变入射粒子的速度大小，使粒子能打到屏上P点，求此情况下入射速度大小的所有可能值。

4、计算题  (12分)如图所示，在以等边三角形abc为边界的区域内，有相互垂直的匀强电场和匀强磁场，磁感应强度为B=1T，磁场方向垂直于abc平面向里。其中等边三角形边长L=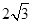m，P、Q分别是ac、bc的中点。一带正电的粒子（不计重力）从ab边中点O沿Oc方向以速度射入，带电粒子恰好做匀速直线运动，从c点射出。

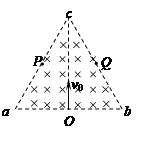
(1)求电场强度的大小和方向；
(2)若仅撤去磁场，带电粒子仍从O点以相同的速度射入，经过t=0.5s恰好从区域的边界中点Q射出。求粒子比荷q/m的大小；
(3)若仅撤去电场，带电粒子仍从O点同方向射入，且恰好也从区域的边界另一中点P射出，求粒子速度v的大小。

5、选择题  如图所示，在圆形区域内有方向垂直向里的匀强磁场．有一束速率各不相同的质子自A点沿半径方向射入磁场，这些质子在磁场中

A．速度越大的，运动时间越长
B．运动时间越长的，其轨迹越长
C．速度越大的，速度的偏转角越小
D．所有质子在磁场中的运动时间相同