1、计算题 如图(a)所示,在空间有一坐标系xoy,直线OP与x轴正方向的夹角为30°,第一象限内有两个方向都垂直纸面向外的匀强磁场区域Ⅰ和Ⅱ,直线OP是它们的边界,OP上方区域Ⅰ中磁场的磁感应强度为B,一质量为m,电荷量为+q的质子(不计重力及质子对磁场的影响)以速度v从O点沿与OP成30°角的方向垂直磁场进入区域Ⅰ,质子先后通过磁场区域Ⅰ和Ⅱ后,恰好垂直于x轴进入第四象限,第四象限存在沿-x轴方向的特殊电场,电场强度E的大小与横坐标x的关系如图(b)所示,试求:
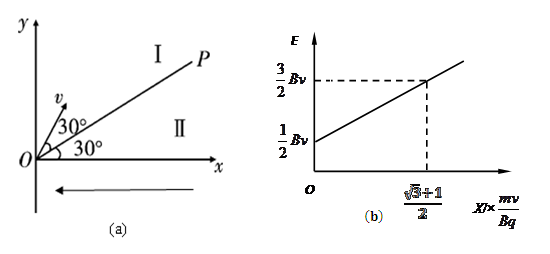
(1)区域Ⅱ中磁场的磁感应强度大小 ;
(2)质子再次到达y轴时的速度大小和方向。
参考答案: (1) ;(2)
;(2)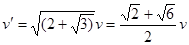 ;方向向左下方与y轴负向成
;方向向左下方与y轴负向成 (
(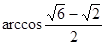 )的夹角
)的夹角
本题解析:
试题分析: (1)由几何关系知:质子再次回到OP时应平行于x轴正向进入Ⅱ区,设质子从OP上的C点进入Ⅱ区后再从D点垂直x轴进入第四象限,轨迹如图。
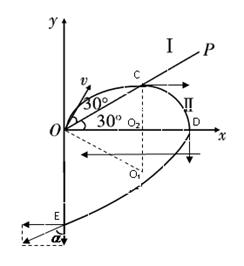
由几何关系可知:O1C⊥OX,O1C与OX的交点O2即为Ⅱ内圆弧的圆心,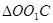 等边三角形。
等边三角形。
设质子在Ⅰ区圆运动半径为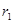 ,在Ⅱ区圆运动半径为
,在Ⅱ区圆运动半径为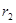 ,
,
则: 由
由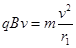
得: , 同理得:
, 同理得:
即区域Ⅱ中磁场的磁感应强度:
(2)D点坐标: 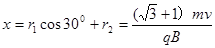
质子从D点再次到达y轴的过程,

设质子再次到达y轴时的速度大小为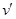 ,
,
由动能定理: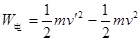 得:
得: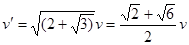
因粒子在y轴方向上不受力,故在y轴方向上的分速度不变
如图有: 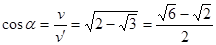
即方向向左下方与y轴负向成 (
(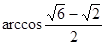 )的夹角
)的夹角
考点: 带电粒子在磁场中的运动
本题难度:困难
2、选择题 如图所示,带正电的电荷固定于Q点,电子在静电力作用下沿顺时针方向做以Q点为焦点的椭圆运动,O为椭圆的中心,M、P、N为椭圆上的三点,M和N分别是轨道上离Q点最近和最远的点,则电子在运动的过程中 ( )
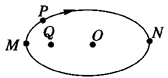
A 在M点的速率最小 B 在N点的电势能最小
C 在P点受的库仑力方向指向O点 D 椭圆上N点的电势最低
参考答案:D
本题解析:电子在运动过程中电势能和动能之和守恒,在在M点的速率最大,在N点的电势能最大,在P点受的库仑力方向指向Q点,负电荷电势越低电势能越大,N点电势能最大,电势最低,选D
本题难度:一般
3、选择题 如右图所示,实线是一个电场中的电场线,虚线是一个负检验电荷在这个电场中的轨迹,若电荷是从a处运动到b处,以下判断正确的是?(?)
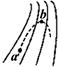
A.电荷从a到b加速度减小
B.b处电势能大
C.b处电势高
D.电荷在b处速度小
参考答案:BD
本题解析:由图可知,b处的电场线比a处的电场线密,说明b处的场强大于a处的场强。根据牛顿第二定律,检验电荷在b处的加速度大于在a处的加速度,A选项不正确;由图可知,电荷做曲线运动,必受到不等于零的合外力,即F电≠0,且F电的方向应指向运动轨迹的内侧。因为检验电荷带负电,所以电场线指向是从疏到密。再利用“顺着电场线电势越来越低”判断a,b处电势高低关系是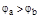 ,C选项不正确;根据检验电荷的位移与所受电场力的夹角大于90°,可知电场力对检验电荷做负功。功是能量变化的量度,可判断由a→b电势能增加,B选项正确;系统的能量守恒,电势能增加则动能减小,速度减小,D选项正确。
,C选项不正确;根据检验电荷的位移与所受电场力的夹角大于90°,可知电场力对检验电荷做负功。功是能量变化的量度,可判断由a→b电势能增加,B选项正确;系统的能量守恒,电势能增加则动能减小,速度减小,D选项正确。
本题难度:一般
4、选择题 如图所示,闭合开关S后A、B板间产生恒定电压U0,已知两极板的长度均为L,带负电的粒子(重力不计)以恒定的初速度V0,从上板左端点正下方h处,平行极板射入电场,恰好打在上板的右端C点。若将下板向上移动距离为板间距的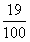 倍,带电粒子将打在上板上的C"点,则B板上移后?
倍,带电粒子将打在上板上的C"点,则B板上移后?

[? ]
A. 粒子在板间的运动时间不变?
B. 粒子打在A板上的动能变大
C. 粒子在A板上的落点C"与极板右端C的距离为板长的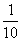
D. 比原入射点低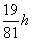 处的入射粒子恰好能打在上板右端C点
处的入射粒子恰好能打在上板右端C点
参考答案:BCD
本题解析:
本题难度:一般
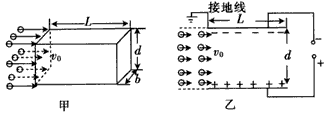
5、计算题 如图甲所示,静电除尘装置中有一长为L、宽为b、高为d的矩形通道,其前、后面板使用绝缘材料,上、下面板使用金属材料。图乙是装置的截面图,上、下两板与电压恒定的高压直流电源相连。质量为m、电荷量为-q、分布均匀的尘埃以水平速度v0进入矩形通道,当带负电的尘埃碰到下板后其所带电荷被中和,同时被收集。通过调整两板间距d可以改变收集效率η。当d=d0时,η为81%(即离下板0.81d0范围内的尘埃能够被收集)。不计尘埃的重力及尘埃之间的相互作用。
(1)求收集效率为100%时,两板间距的最大值dm;
(2)求收集效率η与两板间距d的函数关系;
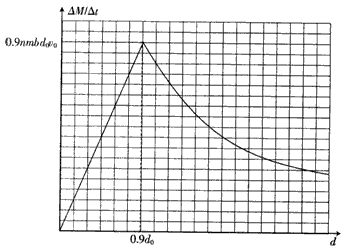
(3)若单位体积内的尘埃数为n,求稳定的工作时单位时间下板收集的尘埃质量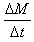 与两板间距d的函数关系,并绘出图线。
与两板间距d的函数关系,并绘出图线。
参考答案:解:(1)收集效率η为81%,即离下板0.81d0的尘埃恰好到达下板的右端边缘,设高压电源的电压为U,则
在水平方向有:L=V0t
在竖直方向有: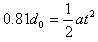
其中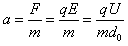
当减小两板间距时,能够增大电场强度,提高装置对尘埃的收集效率。收集效率恰好为100%时,两板间距即为dm甲,如果进一步减小d,收集效率仍为100%。因此
在水平方向有:L=v0t
在竖直方向有: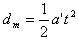
其中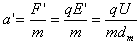
联立以上各式可得:dm=0.9d0
(2)通过前面的求解可知,当d≤0.9d0时,收集效率η均为100%
当d>0.9d0时,设距下板x处的尘埃恰好到达下板的右端边缘,此时有: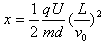
根据题意,收集效率为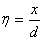
可得:
(3)稳定工作时单位时间下板收集的尘埃质量为: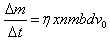
当d≤0.9d0时,η=1,因此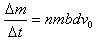
当d>0.9d0时,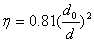 ,因此
,因此
绘出图线如下
本题解析:
本题难度:困难