1、选择题 如图所示,以直角三角形AOC为边界的有界匀强磁场区域,磁感应强度为B,∠A=60°,AO=L,在O点放置一个粒子源,可以向各个方向发射某种带负电粒子(不计重力作用),粒子的比荷为q/m,发射速度大小都为v0,且满足v0=qBL/m。粒子发射方向与OC边的夹角为θ,对于粒子进入磁场后的运动,下列说法正确的是(? )
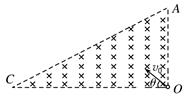
A.粒子有可能打到A点
B.以θ=60°飞入的粒子在磁场中运动时间最短
C.以θ<30°飞入的粒子在磁场中运动的时间都相等
D.在AC边界上只有一半区域有粒子射出
参考答案:AD
本题解析:根据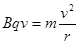 ,又v0=qBL/m,可得
,又v0=qBL/m,可得 ,又OA=L,所以当θ=60o时,粒子经过A点,所以A正确;根据粒子运动 的时间
,又OA=L,所以当θ=60o时,粒子经过A点,所以A正确;根据粒子运动 的时间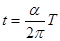 ,圆心角越大,时间越长,粒子以θ=60°飞入磁场中时,粒子从A点飞出,轨迹圆心角等于60o,圆心角最大,运动的时间最长,所以B错误;当粒子沿θ=0°飞入磁场中,粒子恰好从AC中点飞出,在磁场中运动时间也恰好是
,圆心角越大,时间越长,粒子以θ=60°飞入磁场中时,粒子从A点飞出,轨迹圆心角等于60o,圆心角最大,运动的时间最长,所以B错误;当粒子沿θ=0°飞入磁场中,粒子恰好从AC中点飞出,在磁场中运动时间也恰好是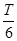 ,θ从0°到60°在磁场中运动时间先减小后增大,在AC边上有一半区域有粒子飞出,所以C错误;D正确。
,θ从0°到60°在磁场中运动时间先减小后增大,在AC边上有一半区域有粒子飞出,所以C错误;D正确。
本题难度:一般
2、选择题 某电子在一匀强磁场中沿垂直于磁场方向运动,以下说法正确的是
A.电子的运动轨迹为一抛物线
B.电子的运动轨迹为一圆周
C.磁场强弱不会影响轨迹
D.电子速度大小不会影响轨迹
参考答案:B
本题解析:电子受到的洛伦兹力方向一直和速度方向垂直,故电子的运动轨迹一定是一个圆,A错误B正确,根据公式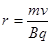 可得,B的大小,v的大小对轨迹的半径有影响,CD错误,
可得,B的大小,v的大小对轨迹的半径有影响,CD错误,
点评:做本题的关键是理解洛伦兹力方向和速度的方向的关系已经对公式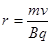 的正确掌握
的正确掌握
本题难度:简单
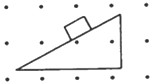
3、选择题 如图所示,已知一带负电的滑块从粗糙斜面的顶端静止下滑,滑至底端时的速率为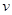 。若加上一个垂直纸面向外的匀强磁场,,同样让它从粗糙斜面的顶端静止下滑,则它滑至底端时的速率与
。若加上一个垂直纸面向外的匀强磁场,,同样让它从粗糙斜面的顶端静止下滑,则它滑至底端时的速率与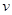 相比(?)
相比(?)
A.变大
B.变小
C.不变
D.条件不足,无法判断
参考答案:B
本题解析:本题考查动能定理的应用、共点力平衡条件
未加磁场时,根据动能定理,有mgh-Wf=.加磁场后,多了洛伦兹力,洛伦兹力不做功,但正压力变大,摩擦力变大,根据动能定理,有mgh-Wf′=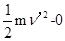 ,Wf′>Wf,所以v′<v.故B正确,A、C、D错误.故选B.
,Wf′>Wf,所以v′<v.故B正确,A、C、D错误.故选B.
本题难度:简单
4、选择题 一不计重力的带正电粒子沿纸面竖直向下飞入某一磁场区域,在竖直平面上运动轨迹如图所示,则该区域的磁场方向是

A.沿纸面水平向右
B.沿纸面水平向左
C.垂直向外
D.垂直向里
参考答案:D
本题解析:带电粒子在磁场中受到洛伦兹力,根据左手定则可得,磁场的方向垂直向里,D正确。
本题难度:简单
5、简答题 如图所示,在虚线MN的上方存在磁感应强度为B的匀强磁场,方向垂直纸面向内,质子和α粒子以相同的速度v0由MN上的O点以垂直MN且垂直于磁场的方向射入匀强磁场中,再分别从MN上A、B两点离开磁场。已知质子的质量为m,电荷为e,α粒子的质量为4m,电荷为2e。忽略带电粒子的重力及质子和α粒子间的相互作用。求:
(1)A、B两点间的距离。
(2)α粒子在磁场中运动的时间。
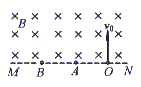
参考答案:(1)?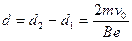 ?
?
(2)
本题解析:(1)质子进入磁场做半径为R1的匀速圆周运动,洛仑兹力提供向心力,根据牛顿第二定律:
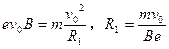 ?(2分)
?(2分)
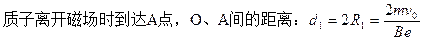 ?(1分)
?(1分)


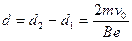 ?(2分)
?(2分)

 ?(2分)
?(2分)
本题难度:一般