1、选择题  两颗人造卫星A、B绕地球做圆周运动，周期之比为TA：TB=1：8，则轨道半径之比和运动速率之比分别为（　　）
A．RA：RB=4：1，VA：VB=1：2
B．RA：RB=4：1，VA：VB=2：1
C．RA：RB=1：4，VA：VB=2：1
D．RA：RB=1：4，VA：VB=1：2

参考答案：人造卫星绕地球做匀速圆周运动，根据万有引力提供向心力，设卫星的质量为m、轨道半径为r、地球质量为M，有
F=F向
F=GMmr2
F向=mv2r=mω2r=m（2πT）2r
因而
GMmr2=mv2r=mω2r=m（2πT）2r=ma
解得
v=

本题解析：

本题难度：一般

2、选择题  质量为m的探月航天器在接近月球表面的轨道上飞行，其运动视为匀速圆周运动。已知月球质量为M，月球半径为R，月球表面重力加速度为g，引力常量为G，不考虑月球自转的影响，则航天器的
[? ]
A.线速度?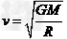
B.角速度?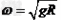
C.运行周期?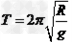
D.向心加速度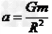

参考答案：AC

本题解析：

本题难度：一般

3、选择题  “嫦娥二号”卫星发射时，长征三号丙火箭直接将卫星由绕地轨道送入200～38×104 km的椭圆奔月轨道，减少了多次变轨麻烦，及早进入绕月圆形轨道，则在“嫦娥奔月”过程中
[? ]
A.离开地球时，地球的万有引力对卫星做负功，重力势能增加；接近月球时月球引力做正功，引力势能减小
B．开始在200 km近地点时，卫星有最大动能
C．在进入不同高度的绕月轨道时，离月球越近，运动的线速度越大，角速度越小
D．在某个绕月圆形轨道上，如果发现卫星高度偏高，可以通过向前加速实现纠偏

参考答案：AB

本题解析：

本题难度：一般

4、选择题  我国发射的“嫦娥一号”探测卫星沿地月转移轨
道到达月球，在距月球表面200km的P点进行第一次“刹车制动”后被月球捕获，进入椭圆轨道Ⅰ绕月飞行，如图所示。之后，卫星在P点又经过两次“刹车制动”，最终在距月球表面200km的圆形轨道Ⅲ上绕月球做匀速圆周运动。则下面说法正确的是

A．卫星在轨道Ⅲ上运动到P点的速度大于沿轨道Ⅰ运动到P点时的速度
B．如果已知“嫦娥一号” 在轨道Ⅲ运动的轨道半径、周期和引力常数G就可以求出月球的质量
C．卫星在轨道Ⅱ上运动时在P点受的万有引力小于该点所需的向心力。
D．卫星在轨道Ⅲ上运动到P点的加速度等于沿轨道Ⅰ运动到P点时的加速度

参考答案：BCD

本题解析：卫星从轨道Ⅲ运动到轨道Ⅰ做离心运动，速度增大；选项A错误；根据题意 “嫦娥一号”运行的半径设其为R，设月球的质量为M，“嫦娥一号”的质量为m，则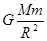=mω2R，解得M=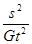；卫星在轨道Ⅱ上运动时在P点，做离心运动，所以万有引力小于该点所需的向心力；卫星在轨道Ⅲ上在P点和在轨道Ⅰ在P点的万有引力大小相等，根据牛顿第二定律，加速度相等，故选BCD
点评：本题难度较小，注意变轨运动速度变化与稳定运行的速度变化完全不同，应用离心运动和向心运动思路理解

本题难度：一般

5、简答题  在“北斗”卫星导航系统中，同步卫星起到非常重要的作用，这些卫星运动在离地心的距离为r的圆形轨道上．已知某颗卫星的质量m，引力常量G，地球自转周期为T，请根据以上信息，求出下列物理量（用题中给出的物理量表示）．
（1）同步卫星运动的角速度大小；
（2）地球对该卫星的吸引力大小；
（3）地球的质量大．

参考答案：（1）已知同步卫星的周期与地球自转的周期相同，即为T，则据角速度与周期的关系有同步卫星的角速度
ω=2πT
（2）地球对卫星的吸引力提供卫星圆周运动的向心力，所以地球对卫星吸引力
F=F向=mrω2=4π2mrT2
（3）地球对卫星的万有引力提供圆周运动的向心力故有：
GmMr2=mr4π2T2
所以地球的质量M=4π2r3GT2
答：（1）同步卫星的角速度为ω=2πT
（2）地球对卫星的吸引力F=4π2mrT2
（3）地球的质量为M=4π2r3GT2

本题解析：

本题难度：一般