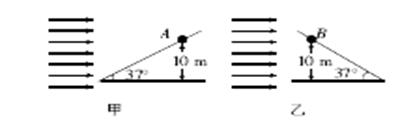
1、计算题  两根完全相同的光滑细直杆上各套有一个完全相同的小球，且两杆均与水平面成角放置，将两小球均从离地面10m高处由静止释放，如图甲、乙所示。在水平向右的风力作用下，A球保持静止，B球沿细直杆下滑。求B球滑到地面所需的时间。（结果保留三位有效数字）（）

参考答案：1.67s

本题解析：设风力为F，对A受力分析后由平衡条件得：

解得：风力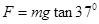
对B受力分析，由牛顿第二定律得：

解得B运动的加速度：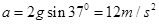
由运动学公式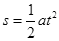
由几何关系得：
解得B下滑所用时间：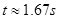

本题难度：一般

2、简答题  甲、乙两车均沿同一平直公路同向行驶．初始时刻，甲车在乙车前方s0=75m处．甲车始终以v1=10m/s的速度匀速运动．乙车作初速度为零，加速度a=2m/s2的匀加速直线运动．求：
（1）乙车追上甲车之前，两车之间的最大距离sm；
（2）经过多少时间t，乙车追上甲车？
（3）乙车一追上甲车，乙车就立即刹车，减速过程加速度大小a"=5m/s2，则再经过多少时间t"甲、乙两车再次相遇．

参考答案：（1）两车速度相等时，相距最远，用时为t1，则：
v1=at1①
两车距离sm=s0+v1t1-12at21②
由①②得：sm=100m
（2）乙车追上甲车用时为t，此间比加车多走s0，即：
12at2-v1t=s0
解得：t=15s
（3）设乙车追上甲车时速度为v2，则：
v2=at=2×15m/s=30m/s
设从刹车到停止所用时间为t2，则：
t2=v2a′=305s=6s
设两车再次相遇用时t3，应满足：
v1t3=v2t3-12a′t23
解得：t3=8s＞6s
所以，乙车停下后，甲车才追上，故乙车此后行驶距离：
s=v2t22=30×62m=90m
时间：t′=sv1=9010s=9s
答：（1）乙车追上甲车之前，两车之间的最大距离100m
（2）经过多15s乙车追上甲车
（3）再经过9s甲、乙两车再次相遇

本题解析：

本题难度：一般

3、简答题  质点从O点起由静止开始做匀加速直线运动，依次通过A、B、C三点，已知质点由O到A经历的时间为1s，OA的距离为4m，
（1）若质点由A到B经历的时间为2s，由B到C经历的时间为1s，求BC的距离；
（2）若AB的距离为2m，BC的距离为4m，求质点由B运动到C经历的时间．

参考答案：（1）第1s内，根据位移时间关系公式，有：xOA=12at21，解得a=2xOAt21=2×41=8m/s2；
OB段位移：xOB=12at32=12×8m×9=36m；
OC段位移：xOC=12at23=12×8×16=64m；
故BC段的位移为：xBC=xOC-xOB=64m-36m=28m；
（2）OB段，根据位移时间关系公式，有：xOB=12at21，解得t1=

本题解析：

本题难度：一般

4、选择题  我校田径运动会上，a、b两同学在操场上沿同一直线运动，为了定量描述他们的运动情况，建立了一直线坐标系，如图甲所示．他们的位置坐标随时间的变化关系如图乙所示，则下列说法中正确的是（　　）
A．6s时，a、b两同学到达的位置相同
B．2s时a同学的速度大于b同学的速度
C．a、b两同学的运动方向相同
D．0-6s内a同学通过的位移小于b同学通过的位移