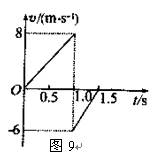
1、简答题  一质量为2 kg的物体（视为质点）从某一高度由静止下落，与地面相碰后（忽略碰撞时间）又上升到最高点，该运动过程的v-t 图象如图9所示，如果上升和下落过程中空气阻力大小相等，求：

（1）物体上升的最大高度；
（2）物体下落过程中所受的空气阻力的大小（取g=10m/s2) 。

参考答案：
（1）1.5米?（2）4N

本题解析：
（1）由图像可知上升的最大高度1.5m。
（2）由图可知下落过程加速度a="8" m/s2
根据牛顿第二定律得mg-Ff=ma
则Ff=mg-ma=20-16=4N。

本题难度：简单

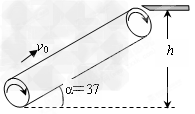
2、计算题  如图所示，电动传送带以恒定速度v0＝1.2m/s运行，传送带与水平面的夹角α＝37°，现将质量m=20kg的物品箱轻放到传送带底端，经过一段时间后，物品箱被送到h=1.8m的平台上，已知物品箱与传送带间的动摩擦因数μ＝0.85，不计其他损耗，则：
（1）每件物品箱从传送带底端送到平台上，需要多少时间？
（2）每输送一个物品箱，电动机需增加消耗的电能是多少焦耳？（g＝10m/s2，sin37°＝0.6）

参考答案：解：（1）物品箱先做匀加速运动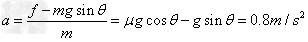
t1＝，s1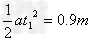＝，可见物品箱之后做匀速运动
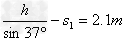s2＝，t2＝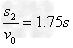
所以?t＝t1＋t2＝3.25s?
（2）每输送一个物品箱，电动机需增加消耗的电能等于物品箱机械能增加量及系统产生的内能

本题解析：

本题难度：一般

3、简答题  图甲中，质量为m的物块A叠放在质量为2m的足够长的木板B上方正中间，木板放在光滑的水平地面上，物块与木板之间的动摩擦因数为μ=0.2．在木板上施加一水平向右的拉力F，在0～3s内F的变化如图乙所示，图中F以mg为单位，重力加速度g=10m/s2．整个系统开始时静止．
（1）分别求出1s末、1.5s末和3s末物块A的速度以及木板B的速度；
（2）在同一坐标系中画出0～3s内木板B和物块A的v-t图象，据此求0～3s内物块相对于木板滑过的距离；
（3）3s末在木板上施加一水平向左的大小F=mg的拉力作用一定时间，使AB最终都能停止运动，求最终A静止在B上的位置．

参考答案：（1）m相对M即将滑动时加速度为am=μg=2m/s2，
则F0=（m+2m）am=0.6mg，是AB相对滑动的临界条件．
在t1=1s时间内，F=mg＞F0．设木板和物块的加速度分别为aA1和aB1，
aA1=fm=μg=2m/s2
aB1=F-f2m=4m/s2
由公式v=at，解得1s末vA1=2m/s，vB1=4m/s
在t2=1.5s时间内，F=0.4mg，vB＞vA，则依然存在相对滑动，
aA2=fm=μg=2m/s2，aB2=F-f2m=1m/s2
由公式v=v0+at，解得得1.5s末vA2=3m/s，vB2=4.5m/s
在t＞1.5s时间内，F=0，vB＞vA，则依然存在相对滑动，aA3=fm=μg=2m/s2，做加速运动．
aB3=f2m=1m/s2，做减速运动．
设经过△t时间共速，
则vA2+aA3△t=vB2-aB3△t
代入数据得△t=0.5s，故2s末以后vA3=vB3=4m/s．
（2）由（1）问计算结果得到物块与木板运动的v-t图象，如图所示．在0～3s内物块相对于木板的距离△s等于木板和物块v-t图线下的面积之差，
即图中带阴影的四边形面积，该四边形由两个三角形组成，上面的三角形面积为0.25（m），下面的三角形面积为2（m），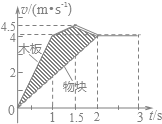
因此物块木板△s=2.25 m．
（3）3s末vA=vB=4m/s，在木板上施加一水平向左的大小F=mg＞F0的拉力后，AB匀减速运动，由-Ft=0-（m+2m）v
得需要作用t=1.2s，才能让AB最终停止运动．
aA=fm=μg=2m/s2，减速，A停止用时tA=vAaA=2s
sA=vA22aA=4m
aB=F-f2m=4m/s2，减速，
t=1.2s时间内，vB"=vB-aBt=-0.8 m/s
t=1.2s末撤去外力F，aB′=f2m=1m/s2，t′=0.8s停止运动．
sB=12(vB+vB′)t-vB′22aB′=1.6m
则△s"=4-1.6=2.4 m，
所以最终A静止在B上的离中间右方2.4-2.25=0.15m位置处．
答：（1）1s末、1.5s末和3s末物块A的速度分别为2m/s、3m/s、4m/s，B的速度分别为4m/s、4.5m/s、4m/s．
（2）图象如图所示，0～3s内物块相对于木板滑过的距离为2.25m．
（3）最终A静止在B上的位置为离中间右方0.15m位置处．

本题解析：

本题难度：一般

4、选择题  某同学在利用斜面研究加速度与力的关系，得到拉力F与小车加速度的a的关系如图所示，若当地的重力加速度为g，不计斜面的摩擦阻力，则根据图像可以求出

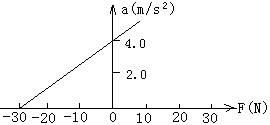
A．小车的质量
B．小车运动的时间
C．斜面倾斜角
D．小车运动的位移

参考答案：A C

本题解析：根据受力分析：，加速度为零时，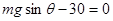
拉力为零时：
解得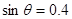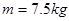，，，所以选AC.

本题难度：简单

5、计算题  （14分）如图所示，足够长的传送带与水平面倾角θ=37°，以12米/秒的速率逆时针转动。在传送带底部有一质量m = 1.0kg的物体，物体与斜面间动摩擦因数μ= 0.25，现用轻细绳将物体由静止沿传送带向上拉动，拉力F = 10.0N，方向平行传送带向上。经时间t = 4.0s绳子突然断了，（设传送带足够长）求：

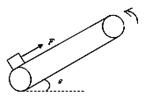
（1）绳断时物体的速度大小；
（2）绳断后物体还能上行多远；
（3）从绳断开始到物体再返回到传送带底端时的运动时间。?（g = 10m/s2，sin37°= 0.6，cos37°= 0.8，）

参考答案：（1）8.0m/s (2) 4.0m(3)3.3s

本题解析：（1）物体开始向上加速运动，受重力mg，摩擦力Ff，拉力F，设加速度为a1，
F – mgsinθ－ Ff = ma1?
Ff = μFN ?
FN = mgcosθ?
得a1 =" 2.0m" / s2 ?（2分）?
t = 4.0s时物体速度v1 =a1t?=" 8.0m/s" ?（1分）
(2) 绳断时,物体距传送带底端s1 =a1t 2 /2= 16m.?
设绳断后? -mgsinθ- μmgcosθ= ma2?
?a2 =" -8.0m" / s2 ?（2分）
t2 = -= 1.0s? ?（2分）
减速运动位移s2=v1t2+ a2t2 2 /2=4.0m?（2分）
(3)物体加速下滑, mgsinθ＋ μmgcosθ= ma2?
a3 =" 8.0m" / s2 ?
当物体与传送带共速时向下运动距离s3=v2/(2a3)=9m?（2分）
用时t3 =" v" / 3=1.5s?（2分）
共速后摩擦力反向，由于mgsinθ 大于 μmgcosθ，物体继续加速下滑
?
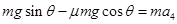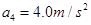
下滑到传送带底部的距离为
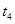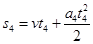设下滑时间为由得

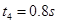
得：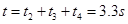
本题考查牛顿第二定律的应用，物体向上运动过程中由拉力重力沿斜面向下的分力和摩擦力提供加速度，由运动学公式可求得4s末的速度大小，绳子断后，物体沿传动带向上减速运动，由重力和摩擦力提供加速度，再由运动学公式求得运动时间，由位移和时间的关系求得位移大小

本题难度：一般